
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:101网校同步练习 高一数学 人教社(新课标B 2004年初审通过) 人教实验版 题型:013
已知函数y=Asin(ωx+![]() )在同一周期内,当x=
)在同一周期内,当x=![]() 时,y最大=2,当x=
时,y最大=2,当x=![]() 时,y最小=-2,那么函数的解析式为
时,y最小=-2,那么函数的解析式为
A.y=2sin(2x+![]() )
)
B.y=2sin(2x-![]() )
)
C.y=2sin(2x+![]() )
)
D.y=2sin(2x-![]() )
)
查看答案和解析>>
科目:高中数学 来源:“伴你学”新课程 数学·必修3、4(人教B版) 人教B版 题型:013
把函数y=f(x)图象上每点向右平移![]() 个单位,再向上平移2个单位,得到的图象对应的函数解析式为y=sin(2x-
个单位,再向上平移2个单位,得到的图象对应的函数解析式为y=sin(2x-![]() ),则f(x)=
),则f(x)=
A.-cos(2x-![]() )+2
)+2
B.-cos(2x-![]() )-2
)-2
C.sin2x-2
D.sin2x+2
查看答案和解析>>
科目:高中数学 来源:四川省绵阳实验高级中学2011届高三第三次月考理科数学试题 题型:044
已知函数
y=lg(ax2-2x+2).(1)若函数y=lg(ax2-2x+2)的值域为R,求实数a的取值范围;
(2)若a=1且x≤1,求y=lg(ax2-2x+2)的反函数f-1(x);
(3)若方程log2(ax2-2x+2)=2在[![]() ,2]内有解,求实数a的取值范围.
,2]内有解,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年甘肃省高三12月月考理科数学试卷 题型:填空题
有下列命题:
① 函数y=4cos 2x,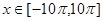 不是周期函数;
不是周期函数;
② 若点P分有向线段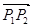 的比为
的比为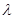 ,且
,且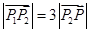 ,则
,则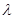 的值为
的值为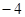 或4;
或4;
③ 函数y=4cos(2x+θ)的图象关于点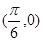 对称的一个必要不充分条件是
对称的一个必要不充分条件是
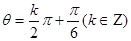 ;
;
④ 函数y= 的最小值为2
的最小值为2 -4
-4
其中正确命题的序号是________.
查看答案和解析>>
科目:高中数学 来源:2013届黑龙江虎林高中高二下学期期中理科数学试卷(解析版) 题型:解答题
已知函数f(x)=alnx-x2+1.
(1)若曲线y=f(x)在x=1处的切线方程为4x-y+b=0,求实数a和b的值;
(2)若a<0,且对任意x1、x2∈(0,+∞),都|f(x1)-f(x2)|≥|x1-x2|,求a的取值范围.
【解析】第一问中利用f′(x)= -2x(x>0),f′(1)=a-2,又f(1)=0,所以曲线y=f(x)在x=1处的切线方程为y=(a-2)(x-1),即(a-2)x-y+2-a=0,
-2x(x>0),f′(1)=a-2,又f(1)=0,所以曲线y=f(x)在x=1处的切线方程为y=(a-2)(x-1),即(a-2)x-y+2-a=0,
由已知得a-2=4,2-a=b,所以a=6,b=-4.
第二问中,利用当a<0时,f′(x)<0,∴f(x)在(0,+∞)上是减函数,
不妨设0<x1≤x2,则|f(x1)-f(x2)|=f(x1)-f(x2),|x1-x2|=x2-x1,
∴|f(x1)-f(x2)|≥|x1-x2|等价于f(x1)-f(x2)≥x2-x1,
即f(x1)+x1≥f(x2)+x2,结合构造函数和导数的知识来解得。
(1)f′(x)= -2x(x>0),f′(1)=a-2,又f(1)=0,所以曲线y=f(x)在x=1处的切线方程为y=(a-2)(x-1),即(a-2)x-y+2-a=0,
-2x(x>0),f′(1)=a-2,又f(1)=0,所以曲线y=f(x)在x=1处的切线方程为y=(a-2)(x-1),即(a-2)x-y+2-a=0,
由已知得a-2=4,2-a=b,所以a=6,b=-4.
(2)当a<0时,f′(x)<0,∴f(x)在(0,+∞)上是减函数,
不妨设0<x1≤x2,则|f(x1)-f(x2)|=f(x1)-f(x2),|x1-x2|=x2-x1,
∴|f(x1)-f(x2)|≥|x1-x2|等价于f(x1)-f(x2)≥x2-x1,即f(x1)+x1≥f(x2)+x2,
令g(x)=f(x)+x=alnx-x2+x+1,g(x)在(0,+∞)上是减函数,
∵g′(x)= -2x+1=
-2x+1= (x>0),
(x>0),
∴-2x2+x+a≤0在x>0时恒成立,
∴1+8a≤0,a≤- ,又a<0,
,又a<0,
∴a的取值范围是
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com