
| A、(-∞,-2012) |
| B、(-2012,0) |
| C、(-∞,-2016) |
| D、(-2016,0) |
| f(x) |
| x2 |
| f(x) |
| x2 |
| x2f(x)-2xf(x) |
| x4 |
| f(x+2014) |
| (x+2014)2 |
| f(-2) |
| (-2)2 |
| f(-2) |
| 4 |


科目:高中数学 来源: 题型:
| 2 |
| A、π | B、2π | C、3π | D、4π |
查看答案和解析>>
科目:高中数学 来源: 题型:
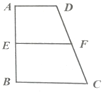 如图,梯形ABCD中,AD∥BC,∠ABC=90°,AD:BC:AB=2:3:4,E、F分别是AB、CD的中点,将四边形ADFE沿直线EF进行翻折.给出四个结论:
如图,梯形ABCD中,AD∥BC,∠ABC=90°,AD:BC:AB=2:3:4,E、F分别是AB、CD的中点,将四边形ADFE沿直线EF进行翻折.给出四个结论:| A、①③ | B、②③ | C、②④ | D、③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:
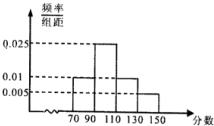 某校1000名学生今年三月“江南十校联考”数学分数的频率分布直方图如图所示,根据该图这1000名学生的数学平均分及众数的估计值分别为( )
某校1000名学生今年三月“江南十校联考”数学分数的频率分布直方图如图所示,根据该图这1000名学生的数学平均分及众数的估计值分别为( )| A、101,90 |
| B、103,100 |
| C、104,100 |
| D、105,110 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com