Question

【题目】已知点A（1，﹣1），B（4，0），C（2，2），平面区域D是所有满足 = +μ （1＜λ≤a，1＜μ≤b）的点P（x，y）组成的区域．若区域D的面积为8，则4a+b的最小值为 （ ）
A.5
B.4
C.9
D.5+4

Answer 1

【答案】C
【解析】解：如图所示，
延长AB到点N，延长AC到点M，使得|AN|=a|AB|，|AM|=b|AC|，作CH∥AN，BF∥AM，NG∥AM，MG∥AN，则四边形ABEC，ANGM，EHGF均为平行四边形．由题意可知：点P（x，y）组成的区域D为图中的四边形EFGH及其内部．
∵ =（3，1）， =（1，3）， =（﹣2，2），∴ = ， = ， =2 ．
∴cos∠CAB= = = ， ．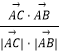
∴四边形EFGH的面积S= =8，
∴（a﹣1）（b﹣1）=1，即 ．
∴4a+b=（4a+b） =5+ =9，当且仅当b=2a=3时取等号．
∴4a+b的最小值为9．
故选：C．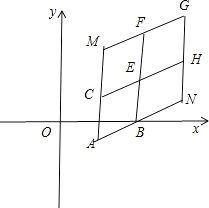

【考点精析】解答此题的关键在于理解基本不等式的相关知识，掌握基本不等式：,（当且仅当时取到等号）；变形公式：，以及对平面向量的基本定理及其意义的理解，了解如果、是同一平面内的两个不共线向量，那么对于这一平面内的任意向量，有且只有一对实数、，使．