【题目】已知直线l：3x﹣4y+t＝0，圆C1经过点A（0，1）与B（2，1），且被y轴的正半轴截得的线段长为2.
（1）求圆C1的方程；
（2）设圆C2是以直线l上的点为圆心的单位圆，若存在圆C2与圆C1有交点，求t的取值范围.
【答案】（1）（x﹣1）2+（y﹣2）2＝2；（2）[10﹣5
，10+5]
【解析】
（1）由题意结合图形求出圆C1的圆心坐标和半径，即可写出圆C1的标准方程；
（2）由题意知直线3x﹣4y+t＝0表示一组平行线，由圆心C1到直线的距离列出不等式，即可求得t的取值范围.
（1）由题意知，被y轴的正半轴截得的线段长为2，故圆过点
，
圆C1经的圆心在线段AB、AD的垂直平分线交点上，
所以圆心坐标为C1（1，2），半径为r1＝
＝，
所以圆C1的标准方程为（x﹣1）2+（y﹣2）2＝2；
（2）由题意知，3x﹣4y+t＝0表示与3x﹣4y＝0平行的一组平行线；
且圆C2是以直线l上的点为圆心的单位圆，
则圆心C1到直线l的距离为d＝
＝
；
若存在圆C2与圆C1有交点，则d≤+1，即≤+1，解得﹣5≤t≤10+5，
所以t的取值范围是[10﹣5，10+5].
轻松课堂单元期中期末专题冲刺100分系列答案科目：高中数学 来源： 题型：
【题目】在平面直角坐标系
中，已知椭圆的方程为：
，动点
在椭圆上，
为原点，线段
的中点为
.
（1）以为极点，
轴的正半轴为极轴，建立极坐标系，求点的轨迹的极坐标方程；
（2）设直线
的参数方程为
（
为参数），与点的轨迹交于
、
两点，求弦长
.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知椭圆
，点
是直线
上的动点，过点作椭圆的切线
，切点为
，
为坐标原点.
（1）若切线的斜率为1，求点的坐标；
（2）求
的面积的最小值，并求出此时的斜率.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，三棱锥S﹣ABC中，SA＝SB＝SC，∠ABC＝90°，AB＞BC，E，F，G分别是AB，BC，CA的中点，记直线SE与SF所成的角为α，直线SG与平面SAB所成的角为β，平面SEG与平面SBC所成的锐二面角为γ，则（ ）
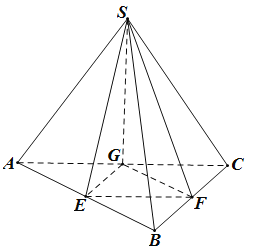
A.α＞γ＞βB.α＞β＞γC.γ＞α＞βD.γ＞β＞α
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知点A（﹣2，1），B（2，4），点P是直线l：y＝x上的动点.
（1）若PA⊥PB，求点P的坐标；
（2）设过A的直线l1与过B的直线l2均平行于l，求l1与l2之间的距离.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】选修4-4：坐标系与参数方程
已知圆锥曲线
（
为参数）和定点
，
、
是此圆锥曲线的左、右焦点，以原点
为极点，以
轴的正半轴为极轴建立极坐标系.
（1）求直线
的直角坐标方程；
（2）经过点
且与直线
垂直的直线
交此圆锥曲线于
、
两点，求
的值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】定义首项为1且公比为正数的等比数列为“M－数列”.
（1）已知等比数列{an}满足：
，求证:数列{an}为“M－数列”；
（2）已知数列{bn}满足:
，其中Sn为数列{bn}的前n项和．
①求数列{bn}的通项公式；
②设m为正整数，若存在“M－数列”{cn}
，对任意正整数k，当k≤m时，都有
成立，求m的最大值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
