
【题目】已知椭圆C:![]() 1(a>b>0),椭圆上的点到焦点的最小距离为
1(a>b>0),椭圆上的点到焦点的最小距离为![]() 且过点P(
且过点P(![]() ,1).
,1).
(1)求椭圆C的方程;
(2)若过点M(3,0)的直线l与椭圆C有两个不同的交点P和Q,若点P关于x轴的对称点为P',判断直线P'Q是否经过定点,如果经过,求出该定点坐标;如果不经过,说明理由.
【答案】(1)![]() .(2)直线P'Q过x轴上定点
.(2)直线P'Q过x轴上定点![]() .
.
【解析】
(1)利用已知条件列出方程组,求出a,b即可得到椭圆方程.
(2)分析当斜率为![]() 时可知定点若存在则必在x轴上,设定点坐标,再设直线方程与P、Q坐标,联立直线与椭圆方程,利用韦达定理,结合三点共线则任意两点的斜率相等列式,进而求出定点坐标即可.
时可知定点若存在则必在x轴上,设定点坐标,再设直线方程与P、Q坐标,联立直线与椭圆方程,利用韦达定理,结合三点共线则任意两点的斜率相等列式,进而求出定点坐标即可.
解:(1)由题意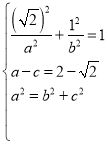 ,解得
,解得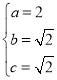 ,
,
故椭圆C的方程为![]() .
.
(2)显然直线![]() 的斜率存在,且当
的斜率存在,且当![]() 斜率为0时, 直线P'Q为x轴.
斜率为0时, 直线P'Q为x轴.
故定点若存在则必在x轴上,设定点为![]() .
.
故设![]() ,
,![]() .
.
将直线与椭圆的方程联立得: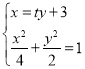 ,
,
消去![]() ,整理得
,整理得![]() .
.
由根与系数之间的关系可得:![]() ,
,![]() .
.
∵点P关于y轴的对称点为P',则P'(x1,﹣y1),且![]() 三点共线
三点共线
∴![]() ,即
,即![]() .
.
即![]() ,
,![]()
整理对![]() ,代入韦达定理有
,代入韦达定理有![]() ,即
,即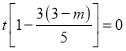 恒成立.解得
恒成立.解得![]() .
.
∴直线P'Q过x轴上定点![]() .
.


 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案科目:高中数学 来源: 题型:
【题目】已知抛物线![]() :
:![]() (
(![]() ),圆
),圆![]() :
:![]() (
(![]() ),抛物线
),抛物线![]() 上的点到其准线的距离的最小值为
上的点到其准线的距离的最小值为![]() .
.
(1)求抛物线![]() 的方程及其准线方程;
的方程及其准线方程;
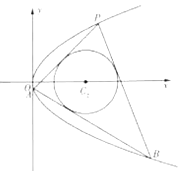
(2)如图,点![]() 是抛物线
是抛物线![]() 在第一象限内一点,过点P作圆
在第一象限内一点,过点P作圆![]() 的两条切线分别交抛物线
的两条切线分别交抛物线![]() 于点A,B(A,B异于点P),问是否存在圆
于点A,B(A,B异于点P),问是否存在圆![]() 使AB恰为其切线?若存在,求出r的值;若不存在,说明理由.
使AB恰为其切线?若存在,求出r的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ,是奇函数.
,是奇函数.
(1)求实数m的值;
(2)画出函数![]() 的图象,并根据图象求解下列问题;
的图象,并根据图象求解下列问题;
①写出函数![]() 的值域;
的值域;
②若函数![]() 在区间
在区间![]() 上单调递增,求实数a的取值范围.
上单调递增,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】作家马伯庸小说《长安十二时辰》中,靖安司通过长安城内的望楼传递信息.同名改编电视剧中,望楼传递信息的方式有一种如下:如图所示,在九宫格中,每个小方格可以在白色和紫色(此处以阴影代表紫色)之间变换,从而一共可以有512种不同的颜色组合,即代表512种不同的信息.现要求每一行,每一列上至多有一个紫色小方格(如图所示即满足要求).则一共可以传递______种信息.(用数字作答)

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}的前n项和为Sn,且Sn=λn2﹣16n+m.
(1)当λ=2时,求通项公式an;
(2)设{an}的各项为正,当m=15时,求λ的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂生产一种产品的原材料费为每件40元,若用x表示该厂生产这种产品的总件数,则电力与机器保养等费用为每件0.05x元,又该厂职工工资固定支出12500元.
(1)把每件产品的成本费P(x)(元)表示成产品件数x的函数,并求每件产品的最低成本费;
(2)如果该厂生产的这种产品的数量x不超过3000件,且产品能全部销售,根据市场调查:每件产品的销售价Q(x)与产品件数x有如下关系:![]() ,试问生产多少件产品,总利润最高?(总利润=总销售额-总的成本)
,试问生产多少件产品,总利润最高?(总利润=总销售额-总的成本)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直三棱柱![]() 中,
中,![]() ,
,![]() ,
,![]() 为
为![]() 的中点.
的中点.

(I)若![]() 为
为![]() 上的一点,且
上的一点,且![]() 与直线
与直线![]() 垂直,求
垂直,求![]() 的值;
的值;
(Ⅱ)在(I)的条件下,设异面直线![]() 与
与![]() 所成的角为45°,求直线
所成的角为45°,求直线![]() 与平面
与平面![]() 成角的正弦值.
成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在中国,“女排精神”概括的是顽强战斗、勇敢拼搏精神.在某年度排球超级杯决赛中,中国女排与俄罗斯女排相遇,已知前四局中,战成了![]() ,且在决胜局中,中国队与俄罗斯队战成了
,且在决胜局中,中国队与俄罗斯队战成了![]() ,根据中国队与俄罗斯队以往的较量,每个球中国队获胜的概率为
,根据中国队与俄罗斯队以往的较量,每个球中国队获胜的概率为![]() ,假定每个球中国队是否获胜相互独立,则再打不超过4球,中国队获得比赛胜利的概率为( )
,假定每个球中国队是否获胜相互独立,则再打不超过4球,中国队获得比赛胜利的概率为( )
(注:排球的比赛规则为5局3胜制,即比赛双方中的一方先拿到3局胜利为获胜队,其中前四局为25分制,即在一方先得到25分,且与对方的分差大于或等于2分,则先拿到25分的一方胜;若一方拿到25分后,但双方分差小于2分,则比赛继续,直到一方领先2分为止;若前四局打成![]() ,则决胜局采用15分制.)
,则决胜局采用15分制.)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
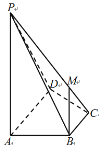
【题目】如图,在四棱锥![]() 中,
中,![]() 、
、![]() 、
、![]() 两两垂直,
两两垂直,![]() ,
,![]() ,
,![]() ,
,![]() 为线段
为线段![]() 上一点(端点除外).
上一点(端点除外).
(1)若异面直线![]() 、
、![]() 所成角的余弦值为
所成角的余弦值为![]() ,求
,求![]() 的长;
的长;
(2)求二面角![]() 的平面角的余弦值.
的平面角的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com