
���� ��1�������оٷ�ȷ�������¼�����������y=f��x��������[1��+�ޣ������������ĸ��ʣ�
��2������$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��ʾ������x������������С��$\frac{\sqrt{3}}{2}$����Բ����$\left\{\begin{array}{l}{{a}^{2}��{b}^{2}}\\{\frac{\sqrt{{a}^{2}-{b}^{2}}}{a}��\frac{\sqrt{3}}{2}}\end{array}\right.$�������$\left\{\begin{array}{l}{a��b}\\{a��2b}\end{array}\right.$����a��[1��5]��b��[2��4]���������㲻��ʽ���ƽ��������������ȣ�������$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��ʾ������x������������С��$\frac{\sqrt{3}}{2}$����Բ�ĸ��ʣ�
��� �⣺��1���ߺ���f��x��=ax2-4bx+1��ͼ��ĶԳ���Ϊֱ��x=$\frac{2b}{a}$��Ҫʹf��x��=ax2-4bx+1������[1��+�ޣ���Ϊ�����������ҽ���a��0��$\frac{2b}{a}$��1����2b��a������2�֣�
��a=1����b=-1��
��a=2����b=-1��1��
��a=3����b=-1��1��
���¼����������¼��ĸ�����1+2+2=5������4�֣�
���������������ԣ�a��b������3��5=15��
�������¼��ĸ���Ϊ$\frac{5}{15}$=$\frac{1}{3}$������6�֣�
��2������$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��ʾ������x������������С��$\frac{\sqrt{3}}{2}$����Բ����$\left\{\begin{array}{l}{{a}^{2}��{b}^{2}}\\{\frac{\sqrt{{a}^{2}-{b}^{2}}}{a}��\frac{\sqrt{3}}{2}}\end{array}\right.$����8�֣�
�����$\left\{\begin{array}{l}{a��b}\\{a��2b}\end{array}\right.$
��a��[1��5]��b��[2��4]���������㲻��ʽ���ƽ��������ͼ��Ӱ������ʾ��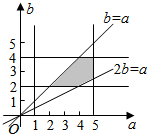 ����10�֣�
����10�֣�
��Ӱ���ֵ����Ϊ$\frac{15}{4}$��������ĸ���P=$\frac{15}{32}$������12�֣�
���� ���⿼����ʵļ��㣬����ѧ���ļ����������������������ǹؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{2}$ | B�� | $\frac{{\sqrt{2}}}{2}$ | C�� | $-\frac{{\sqrt{2}}}{2}$ | D�� | $-\frac{1}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ����ԭ��Գ� | B�� | x��Գ� | C�� | y��Գ� | D�� | ֱ��y=x�Գ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com