
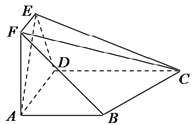
【题目】在如图所示的多面体![]() 中,
中, ![]() 为直角梯形,
为直角梯形, ![]() ,
, ![]() ,四边形
,四边形![]() 为等腰梯形,
为等腰梯形, ![]() ,已知
,已知![]() ,
, ![]() ,
, ![]() .
.
(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
科目:高中数学 来源: 题型:
【题目】《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有刍甍,下广三丈,袤四丈,上袤二丈,无广,高二丈,问积几何?”其意思为:“今有底面为矩形的屋脊状的锲体,下底面宽3丈,长4丈,上棱长2丈,高2丈,问:它的体积是多少?”已知1丈为10尺,该锲体的三视图如图所示,则该锲体的体积为( )
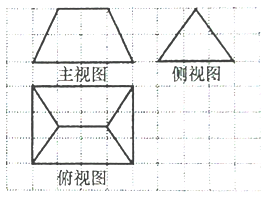
A. 10000立方尺 B. 11000立方尺 C. 12000立方尺 D. 13000立方尺
查看答案和解析>>
科目:高中数学 来源: 题型:
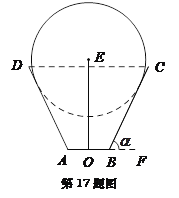
【题目】一儿童游乐场拟建造一个“蛋筒”型游乐设施,其轴截面如图中实线所示. ![]() 是等腰梯形,
是等腰梯形, ![]() 米,
米, ![]() (
(![]() 在
在![]() 的延长线上,
的延长线上, ![]() 为锐角). 圆
为锐角). 圆![]() 与
与![]() 都相切,且其半径长为
都相切,且其半径长为![]() 米.
米. ![]() 是垂直于
是垂直于![]() 的一个立柱,则当
的一个立柱,则当![]() 的值设计为多少时,立柱
的值设计为多少时,立柱![]() 最矮?
最矮?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() :
: ![]() (
(![]() ),设
),设![]() 为圆
为圆![]() 与
与![]() 轴负半轴的交点,过点
轴负半轴的交点,过点![]() 作圆
作圆![]() 的弦
的弦![]() ,并使弦
,并使弦![]() 的中点恰好落在
的中点恰好落在![]() 轴上.
轴上.
(Ⅰ)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(Ⅱ)延长![]() 交曲线
交曲线![]() 于点
于点![]() ,曲线
,曲线![]() 在点
在点![]() 处的切线与直线
处的切线与直线![]() 交于点
交于点![]() ,试判断以点
,试判断以点![]() 为圆心,线段
为圆心,线段![]() 长为半径的圆与直线
长为半径的圆与直线![]() 的位置关系,并证明你的结论.
的位置关系,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】求满足下列条件的直线的方程:
(1)经过两条直线2x﹣3y+10=0和3x+4y﹣2=0的交点,且垂直于直线3x﹣2y+4=0;
(2)经过两条直线2x+y﹣8=0和x﹣2y+1=0的交点,且平行于直线4x﹣3y﹣7=0.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com