
分析 (Ⅰ)根据已知条件列出关于x的x的方程,解方程即可;
(Ⅱ)证法一:由函数$f(x)=\frac{4}{4x+15}$的单调性得到$0<f(x)<\frac{4}{15}$.根据a1=1,an+1=f(an)得到${a_2}=\frac{4}{19},{a_3}=\frac{76}{301}$且0<an≤1.用数学归纳法证明$0<{a_{2n}}<\frac{1}{4}<{a_{2n-1}}≤1$.
证法二:$\frac{{{a_{n+1}}-\frac{1}{4}}}{{{a_{n+1}}+4}}=\frac{{\frac{4}{{4{a_{n+1}}+15}}-\frac{1}{4}}}{{\frac{4}{{4{a_{n+1}}+15}}+4}}=-\frac{1}{4}\frac{{{a_n}-\frac{1}{4}}}{{{a_n}+4}}$,且$\frac{{{a_1}-\frac{1}{4}}}{{{a_1}+4}}=\frac{3}{20}$$\left\{{\frac{{{a_n}-\frac{1}{4}}}{{{a_n}+4}}}\right\}$是以$\frac{3}{20}$为首项,$-\frac{1}{4}$为公比的等比数列.分函数的奇偶性进行推论;
(Ⅲ)证法一:由(2),我们有$\frac{4}{19}≤{a_{2n}}<\frac{1}{4}<{a_{2n-1}}≤1$,从而a1+a2+…+an≤n.
设${b_n}={a_n}-\frac{1}{4}$,
分类讨论:当n=1,2,3时,b1+b2+…+bn>0成立,左边不等式均成立.
当n>3时,有${b_1}+{b_2}+…+{b_n}>{b_1}+{b_3}+\frac{b_2}{{1-{{(\frac{1}{3})}^2}}}=\frac{3}{4}+\frac{3}{1204}+\frac{{-\frac{3}{76}}}{{1-{{(\frac{1}{3})}^2}}}≥0$,易得${a_1}+{a_2}+…+{a_n}>\frac{1}{4}n$.
证法2:由(Ⅱ)可知0<an≤1,推知$\frac{{{b_{n+1}}}}{b_n}=\frac{-1}{{4{b_n}+16}}∈(-1,0)$,故b2n-1+b2n>0.分类讨论:n为奇数和偶数两种情况.
解答 解:(Ⅰ)$f(x)-x=0?\frac{4}{4x+15}=x⇒x=-4或x=\frac{1}{4}$;
(Ⅱ)存在$c=\frac{1}{4}$使得${a_{2n}}<\frac{1}{4}<{a_{2n-1}}$.
证法1:因为$f(x)=\frac{4}{4x+15}$,当x∈(0,1]时,f(x)单调递减,所以$0<f(x)<\frac{4}{15}$.
因为a1=1,
所以由${a_{n+1}}=\frac{4}{{4{a_n}+15}}$得${a_2}=\frac{4}{19},{a_3}=\frac{76}{301}$且0<an≤1.
下面用数学归纳法证明$0<{a_{2n}}<\frac{1}{4}<{a_{2n-1}}≤1$.
因为$0<{a_2}=\frac{4}{19}<\frac{1}{4}<{a_1}=1≤1$,所以当n=1时结论成立.
假设当n=k时结论成立,即$0<{a_{2k}}<\frac{1}{4}<{a_{2k-1}}<1$.
由于$f(x)=\frac{4}{4x+15}$为(0,1]上的减函数,
所以$f(0)>f({a_{2k}})>f(\frac{1}{4})>f({a_{2k-1}})>f(1)$,
从而$\frac{4}{15}>{a_{2k+1}}>\frac{1}{4}>{a_{2k}}>\frac{4}{19}$,
因此$f(\frac{4}{15})<f({a_{2k+1}})<f(\frac{1}{4})<f({a_{2k}})<f(\frac{4}{19})$,
即$0<f(\frac{4}{15})≤{a_{2k+2}}<\frac{1}{4}<{a_{2k+1}}<f(\frac{4}{19})≤1$.
综上所述,对一切n∈N*,$0<{a_{2n}}<\frac{1}{4}<{a_{2n-1}}≤1$都成立,
即存在$c=\frac{1}{4}$使得${a_{2n}}<\frac{1}{4}<{a_{2n-1}}$.
证法2:$\frac{{{a_{n+1}}-\frac{1}{4}}}{{{a_{n+1}}+4}}=\frac{{\frac{4}{{4{a_{n+1}}+15}}-\frac{1}{4}}}{{\frac{4}{{4{a_{n+1}}+15}}+4}}=-\frac{1}{4}\frac{{{a_n}-\frac{1}{4}}}{{{a_n}+4}}$,
且$\frac{{{a_1}-\frac{1}{4}}}{{{a_1}+4}}=\frac{3}{20}$$\left\{{\frac{{{a_n}-\frac{1}{4}}}{{{a_n}+4}}}\right\}$是以$\frac{3}{20}$为首项,$-\frac{1}{4}$为公比的等比数列.
所以$\frac{{{a_n}-\frac{1}{4}}}{{{a_n}+4}}=\frac{3}{20}•{({-\frac{1}{4}})^{n-1}}$.
易知an>0,所以当n为奇数时,${a_n}>\frac{1}{4}$;当n为偶数时,${a_n}<\frac{1}{4}$
即存在$c=\frac{1}{4}$,使得${a_{2n}}<\frac{1}{4}<{a_{2n-1}}$.
(Ⅲ)证明:由(2),我们有$\frac{4}{19}≤{a_{2n}}<\frac{1}{4}<{a_{2n-1}}≤1$,从而a1+a2+…+an≤n.
设${b_n}={a_n}-\frac{1}{4}$,
则由${a_{n+1}}=\frac{4}{{4{a_n}+15}}$得$\frac{{|{{b_{n+1}}}|}}{{|{b_n}|}}=|{\frac{1}{{4({b_n}+1)}}}|=\frac{1}{{4{a_n}+3}}<\frac{1}{3}$.
由于${b_1}=\frac{3}{4},{b_2}=-\frac{3}{76},{b_3}=\frac{3}{1204}$,
因此n=1,2,3时,b1+b2+…+bn>0成立,左边不等式均成立.
当n>3时,有${b_1}+{b_2}+…+{b_n}>{b_1}+{b_3}+\frac{b_2}{{1-{{(\frac{1}{3})}^2}}}=\frac{3}{4}+\frac{3}{1204}+\frac{{-\frac{3}{76}}}{{1-{{(\frac{1}{3})}^2}}}≥0$,
因此${a_1}+{a_2}+…+{a_n}>\frac{1}{4}n$.
从而$\frac{1}{4}n<{a_1}+{a_2}+…+{a_n}≤n$.即$\frac{1}{4}<\frac{S_n}{n}≤1$.
解法2:由(Ⅱ)可知0<an≤1,所以${b_n}={a_n}-\frac{1}{4}∈(-\frac{1}{4},\frac{3}{4}]$${b_{n+1}}={a_{n+1}}-\frac{1}{4}=\frac{4}{{4{a_n}+15}}=\frac{{-{b_n}}}{{4{b_n}+16}}$,
所以$\frac{{{b_{n+1}}}}{b_n}=\frac{-1}{{4{b_n}+16}}∈(-1,0)$
所以b2n-1+b2n>0
所以当n为偶数时,b1+b2+…+bn>0;
所以当n为奇数时,(b1+b2+…+bn-1)+bn>0
即${S_n}-\frac{1}{4}n>0$.
点评 本题考查数列递推式,考查数列的通项,考查数学归纳法,考查学生分析解决问题的能力,难度大.


科目:高中数学 来源: 题型:选择题
| A. | 9,11 | B. | 10,10 | C. | 8,10 | D. | 10,11 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若d1=d2=1,则直线P1P2与直线l平行 | |
| B. | 若d1=1,d2=-1,则直线P1P2与直线l垂直 | |
| C. | 若d1+d2=0,则直线P1P2与直线l垂直 | |
| D. | 若d1•d2≤0,则直线P1P2与直线l相交 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
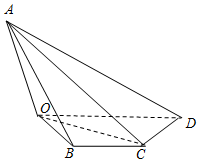 如图,四棱锥A-OBCD中,已知平面AOC⊥面OBCD,AO=2$\sqrt{3}$,OB=BC=2,CD=4,∠OBC=∠BCD=120°.
如图,四棱锥A-OBCD中,已知平面AOC⊥面OBCD,AO=2$\sqrt{3}$,OB=BC=2,CD=4,∠OBC=∠BCD=120°.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
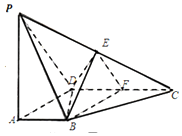 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,∠DAB为直角,AB∥CD,AD=CD=2AB=2,E,F分别为PC,CD的中点.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,∠DAB为直角,AB∥CD,AD=CD=2AB=2,E,F分别为PC,CD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com