已知函数
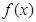
对一切实数
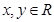
都有
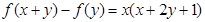
成立,且
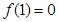
,(1)求
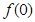
的值;(2)求
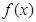
的解析式.
(1)
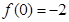
;(2)
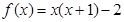
.
本试题主要考查了函数的求解和运用。
(1)解:因为函数
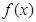
对一切实数
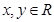
都有
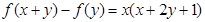
成立,
且
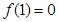
,所以令
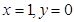
代入上式得
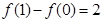
,所以
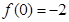
。
(2) 解:因为函数
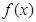
对一切实数
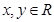
都有
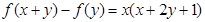
成立,
所以令
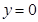
代入上式得
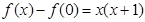
又由(1)知
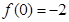
,所以
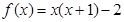
练习册系列答案
相关习题
科目:高中数学
来源:不详
题型:单选题
.定义在
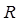
上的函数
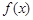
满足
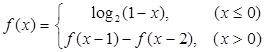
,则
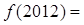
( )
A.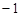 | B.0 | C.1 | D.2 |
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
已知
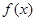
为定义在
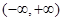
上的可导函数,且
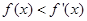
对于
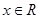
恒成立,且e为自然对数的底,则下面正确的是( )
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
已知函数
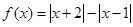
.
(1)试求
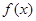
的值域;
(2)设
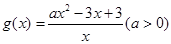
,若对
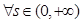
,
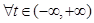
,恒
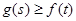
成立,试求实数
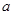
的取值范围
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
若
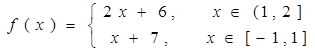
则
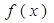
的最大值,最小值分别为( ).
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
设f(x)=
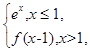
则f(ln3)= ( )
| A.ln3-1 | B.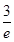 | C.e | D.3e |
查看答案和解析>>
科目:高中数学
来源:不详
题型:填空题
已知f ( x ) =
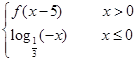
, 则f ( 2012 ) =
;
查看答案和解析>>

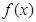 对一切实数
对一切实数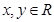 都有
都有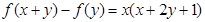 成立,且
成立,且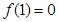 ,(1)求
,(1)求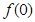 的值;(2)求
的值;(2)求 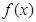 的解析式.
的解析式. 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案