练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】某校高三年级有男生人，编号为，，…，；女生人，编号为，，…，．为了解学生的学习状态，按编号采用系统抽样的方法从这名学生中抽取人进行问卷调查，第一组抽到的号码为，现从这名学生中随机抽取人进行座谈，则这人中既有男生又有女生的概率是（ ）

    A.B.C.D.

    【答案】C

    【解析】

    根据系统抽样的方法分析抽取出来的学生编号,再分析其中男女生的个数,再利用排列组合的方法求解概率即可.

    由题意知,抽取的学生编号成等差数列,首项为10,公差为.

    故抽取的10人中男生有10,70,130,190,这4个号码,其余的6人为女生.

    即抽到的10人中,有男生4人,女生6人,

    再从这10位学生中随机抽取2人座谈,

    基本事件总数,

    2人中既有男生又有女生包含的基本事件个数,

    故2人中既有男生又有女生的概率.

    故选：C

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】某学校高三年级有、两个自习教室，甲、乙、丙名学生各自随机选择其中一个教室自习，则甲、乙两人不在同一教室上自习的概率为________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆()的左、右焦点分别是，，点为的上顶点，点在上，，且.

    （1）求的方程；

    （2）已知过原点的直线与椭圆交于，两点，垂直于的直线过且与椭圆交于，两点，若，求.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】新疆在种植棉花有着得天独厚的自然条件，土质呈碱性，夏季温差大，阳光充足，光合作用充分，生长时间长，这种环境下种植的棉花绒长品质好产量髙，所以新疆棉花举世闻名.每年五月份，新疆地区进入灾害天气高发期，灾害天数对当年棉花产量有着重要影响，根据过去五年的数据统计，得到相关数据如下表:

    灾害天气天数(天)

    2

    3

    4

    5

    8

    棉花产量(吨/公顷)

    3.2

    2.4

    2

    1.9

    1.7

    根据以上数据，技术人员分别借助甲乙两种不同的回归模型，得到两个回归方程，

    方程甲:，方程乙:.

    （1）为了评价两种模型的拟合效果，完成以下任务:① 完成下表；(计算结果精确到0.1)

    ②分别计算模型甲与模型乙的残差平方和及，并比铰的大小，判断哪个模型拟合效果更好?

    灾害天气天数(天)

    2

    3

    4

    5

    8

    棉花产量(吨公顷)

    3.2

    2.4

    2

    1.9

    1.7

    模型甲

    估计值

    2.4

    2.1

    1.6

    残差

    0

    0.1

    模型乙

    估计值

    2.3

    2

    1.9

    残差

    0.1

    0

    0

    （2）根据天气预报，今年五月份新疆市灾害天气是6天的概率是0.5，灾害天气是7天的概率为0.4，灾害天气是10天的概率为0.1，若何女士在新疆市承包了15公顷地种植棉花，请你根据第(1)问中拟合效果较好的模型估计一下何女士今年棉花的产量.(计算过程中所有结果精确到0.01)

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】重庆市的新高考模式为“”，其中“3”是指语文、数学、外语三门必步科目：“1”是指物理、历史两门科目必选且只选一门；“2”是指在政治、地理、化学、生物四科中必须任选两门，这样学生的选科就可以分为两类：物理类与历史类，比如物理类有：物理+化学+生物，物理+化学+地理，物理+化学+政治.物理+政治+地理，物理+政治+生物，物理+生物+地理.重庆某中学高一学生共1200人，其中男生650人，女生550人，为了适应新高考，该校高一的学生在3月份进行了“”的选科，选科情况部分数据如下表所示：（单位：人）

    性别

    物理类

    历史类

    合计

    男生

    590

    女生

    240

    合计

    900

    （1）请将题中表格补充完整，并判断能否有99%把握认为“是否选择物理类与性别有关”？

    （2）已知高一9班和10班选科结果都只有四种组合：物理+化学+生物，物理+化学+地理，政治+历史+地理，政治+历史+生物.现用数字1，2，3，4依次代表这四种组合，两个班的选科数据如下表所示（单位：人）.

    理化生

    理化地

    政史地

    政史生

    班级总人数

    9班

    18

    18

    12

    12

    60

    10班

    24

    12

    18

    6

    60

    现分别从两个班各选一人，记他们的选科结果分别为和，令，用频率代表概率，求随机变量的分布列和期望.（参考数据：，，）

    附：；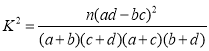

    0.050

    0.025

    0.010

    0.005

    3.841

    5.024

    6.635

    7.879

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某工厂生产某种产品，为了控制质量，质量控制工程师要在产品出厂前对产品进行检验．现有（且）份产品，有以下两种检验方式：（1）逐份检验，则需要检验次；（2）混合检验，将这份产品混合在一起作为一组来检验．若检测通过，则这份产品全部为正品，因而这份产品只要检验一次就够了；若检测不通过，为了明确这份产品究竟哪几份是次品，就要对这份产品逐份检验，此时这份产品的检验次数总共为次．假设在接受检验的样本中，每份样本的检验结果是正品还是次品都是独立的，且每份样本是次品的概率为．

    （1）如果，采用逐份检验方式进行检验，求检测结果恰有两份次品的概率；

    （2）现对份产品进行检验，运用统计概率相关知识回答：当和满足什么关系时，用混合检验方式进行检验可以减少检验次数？

    （3）①当（且）时，将这份产品均分为两组，每组采用混合检验方式进行检验，求检验总次数的数学期望；

    ②当（，且，）时，将这份产品均分为组，每组采用混合检验方式进行检验，写出检验总次数的数学期望（不需证明）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】2019年庆祝中华人民共和国成立70周年阅兵式彰显了中华民族从站起来、富起来迈向强起来的雄心壮志.阅兵式规模之大、类型之全均创历史之最，编组之新、要素之全彰显强军成就.装备方阵堪称“强军利刃”“强国之盾”，见证着人民军队迈向世界一流军队的坚定步伐.此次大阅兵不仅得到了全中国人的关注，还得到了无数外国人的关注.某单位有6位外国人，其中关注此次大阅兵的有5位，若从这6位外国人中任意选取2位做一次采访，则被采访者都关注了此次大阅兵的概率为（ ）

    A.B.C.D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】小明和父母都喜爱《中国好声音》这栏节目，年月日晚在鸟巢进行中国好声音终极决赛，四强选手分别为李荣浩战队的邢晗铭，那英战队的斯丹曼簇，王力宏战队的李芷婷，庾澄庆战队的陈其楠，决赛后四位选手相应的名次为、、、，某网站为提升娱乐性，邀请网友在比赛结束前对选手名次进行预测.现用、、、表示某网友对实际名次为、、、的四位选手名次做出的一种等可能的预测排列，是该网友预测的名次与真实名次的偏离程度的一种描述.

    （1）求的分布列及数学期望；

    （2）按（1）中的结果，若小明家三人的排序号与真实名次的偏离程度都是，计算出现这种情况的概率（假定小明家每个人排序相互独立）.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数有两个不同的极值点.

    （1）求的取值范围.

    （2）求的极大值与极小值之和的取值范围.

    （3）若，则是否有最小值？若有，求出最小值；若没有，说明理由.

    查看答案和解析>>

    同步练习册答案