
| 1 | 2 |
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案科目:高中数学 来源:2013届河北省高二下学期考试文科数学试卷(解析版) 题型:选择题
某同学准备用反证法证明如下问题:函数f(x)在[0,1]上有意义,且f(0)=f(1),如果对于不同的x1,x2∈[0,1]都有|f(x1)-f(x2)|<|x1-x2|,求证:|f(x1)-f(x2)|< ,那么它的假设应该是( ).
,那么它的假设应该是( ).
A.“对于不同的x1,x2∈[0,1],都得|f(x1)-f(x2)|<|x1-x2| 则|f(x1)-f(x2)|≥ ”
”
B. “对于不同的x1,x2∈[0,1],都得|f(x1)-f(x2)|> |x1-x2| 则|f(x1)-f(x2)|≥ ”
”
C.“∃x1,x2∈[0,1],使得当|f(x1)-f(x2)|<|x1-x2| 时有|f(x1)-f(x2)|≥ ”
”
D.“∃x1,x2∈[0,1],使得当|f(x1)-f(x2)|>|x1-x2|时有|f(x1)-f(x2)|≥ ”
”
查看答案和解析>>
科目:高中数学 来源:2009-2010学年度新课标高三上学期数学单元测试12-文科-算法、复数、推理与证明 题型:填空题
某同学准备用反证法证明如下一个问题:函数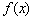 在
在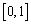 上有意义,且
上有意义,且 ,如果对于不同的
,如果对于不同的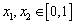 ,都有
,都有 ,求证:
,求证: 。那么他的反设应该是___________.
。那么他的反设应该是___________.
查看答案和解析>>
科目:高中数学 来源:2009-2010学年度新课标高三上学期数学单元测试12-理科-算法、复数、推理与证明 题型:填空题
某同学准备用反证法证明如下一个问题:函数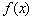 在
在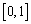 上有意义,且
上有意义,且 ,如果对于不同的
,如果对于不同的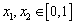 ,都有
,都有 ,求证:
,求证: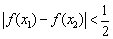 。那么他的反设应该是___________.
。那么他的反设应该是___________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com