
分析 由椭圆的参数方程可得P(3cosα,2sinα)(0<α<$\frac{π}{2}$),则$\frac{1}{9co{s}^{2}α}$+$\frac{1}{4si{n}^{2}α}$=(sin2α+cos2α)($\frac{1}{9co{s}^{2}α}$+$\frac{1}{4si{n}^{2}α}$),展开运用基本不等式可得最小值,再由直角三角形的勾股定理可得斜边的最小值.
解答 解:椭圆$\frac{x^2}{9}+\frac{y^2}{4}$=1,可设P(3cosα,2sinα)(0<α<$\frac{π}{2}$),
则$\frac{1}{9co{s}^{2}α}$+$\frac{1}{4si{n}^{2}α}$=(sin2α+cos2α)($\frac{1}{9co{s}^{2}α}$+$\frac{1}{4si{n}^{2}α}$)
=$\frac{1}{9}$+$\frac{1}{4}$+$\frac{1}{4}$•$\frac{co{s}^{2}α}{si{n}^{2}α}$+$\frac{1}{9}$•$\frac{si{n}^{2}α}{co{s}^{2}α}$≥$\frac{13}{36}$+2$\sqrt{\frac{co{s}^{2}α}{4si{n}^{2}α}•\frac{si{n}^{2}α}{9co{s}^{2}α}}$=$\frac{13}{36}$+$\frac{1}{3}$=$\frac{25}{36}$,
当且仅当2sin2α=3cos2α,即tanα=$\frac{\sqrt{6}}{2}$,取得等号.
由题意可得直角三角形斜边长为$\sqrt{\frac{1}{9co{s}^{2}α}+\frac{1}{4si{n}^{2}α}}$,
即有最小值为$\frac{5}{6}$.
故答案为:$\frac{5}{6}$.
点评 本题考查椭圆的参数方程的运用,考查三角函数的最值的求法,注意运用乘1法,考查基本不等式的运用,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ${(\frac{1}{e})^a}<{(\frac{1}{e})^b}$ | B. | 3b<3a | C. | (lga)2<(lgb)2 | D. | loga3>logb3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
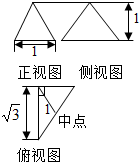 某几何体的三视图如图所示,则它的外接球的体积为( )
某几何体的三视图如图所示,则它的外接球的体积为( )| A. | 4π | B. | $\frac{8}{3}π$ | C. | $\frac{4}{9}π$ | D. | $\frac{4}{3}π$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com