
【题目】如图所示,在梯形![]() 中,
中,![]() ,
,![]() ,四边形
,四边形![]() 为矩形,且
为矩形,且![]() 平面
平面![]() ,
,![]() .
.
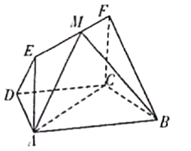
(1)求证:![]() 平面
平面![]() ;
;
(2)点![]() 在线段
在线段![]() 上运动,设平面
上运动,设平面![]() 与平面
与平面![]() 所成锐二面角为
所成锐二面角为![]() ,试求
,试求![]() 的取值范围.
的取值范围.
科目:高中数学 来源: 题型:
【题目】“大众创业,万众创新”是李克强总理在本届政府工作报告中向全国人民发出的口号.共生产企业积极响应号召,大力研发新产品,为了对新研发的一批产品进行合理定价,将该产品按事先拟定的价格进行试销,得到一组销售数据![]() ,如表所示:
,如表所示:
试销单价 | 4 | 5 | 6 | 7 | 8 | 9 |
产品销量 | 90 | 84 | 83 | 80 | 75 | 68 |
已知![]() ,
,![]() .
.
(1)已知变量![]() ,只有线性相关关系,求产品销量
,只有线性相关关系,求产品销量![]() (件)关于试销单价
(件)关于试销单价![]() (元)的线性回方程
(元)的线性回方程![]() ;
;
(2)用![]() 表示用(Ⅱ)中所求的线性回归方程得到的与
表示用(Ⅱ)中所求的线性回归方程得到的与![]() 对应的产品销量的估计值.当销售数据
对应的产品销量的估计值.当销售数据![]() 对应的差的绝对值
对应的差的绝对值![]() 时,则将售数数
时,则将售数数![]() 称为一个“好数据”.现从6小销售数据中任取2个;求“好数据”至少有一个的概率.
称为一个“好数据”.现从6小销售数据中任取2个;求“好数据”至少有一个的概率.
(参考公式:线性回归方程中![]() 的最小二乘估计分别为
的最小二乘估计分别为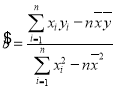 ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,以原点O为极点,x轴的正半轴为极轴建立极坐标系,已知直线l的参数方程为: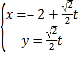 ,
,![]() 为参数
为参数![]() 点的极坐标为
点的极坐标为![]() ,曲线C的极坐标方程为
,曲线C的极坐标方程为![]() .
.
![]() Ⅰ
Ⅰ![]() 试将曲线C的极坐标方程化为直角坐标方程,并求曲线C的焦点在直角坐标系下的坐标;
试将曲线C的极坐标方程化为直角坐标方程,并求曲线C的焦点在直角坐标系下的坐标;
![]() Ⅱ
Ⅱ![]() 设直线l与曲线C相交于两点A,B,点M为AB的中点,求
设直线l与曲线C相交于两点A,B,点M为AB的中点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在![]() 中,已知
中,已知![]() ,
,![]() ,
,![]() ,D是边AC上一点,将
,D是边AC上一点,将![]() 沿BD折起,得到三棱锥
沿BD折起,得到三棱锥![]() .若该三棱锥的顶点A在底面BCD的射影M在线段BC上,设
.若该三棱锥的顶点A在底面BCD的射影M在线段BC上,设![]() ,则x的取值范围为( )
,则x的取值范围为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为践行“绿水青山就是金山银山”的发展理念,某城区对辖区内![]() ,
,![]() ,
,![]() 三类行业共200个单位的生态环境治理成效进行了考核评估,考评分数达到80分及其以上的单位被称为“星级”环保单位,未达到80分的单位被称为“非星级”环保单位.现通过分层抽样的方法获得了这三类行业的20个单位,其考评分数如下:
三类行业共200个单位的生态环境治理成效进行了考核评估,考评分数达到80分及其以上的单位被称为“星级”环保单位,未达到80分的单位被称为“非星级”环保单位.现通过分层抽样的方法获得了这三类行业的20个单位,其考评分数如下:
![]() 类行业:85,82,77,78,83,87;
类行业:85,82,77,78,83,87;
![]() 类行业:76,67,80,85,79,81;
类行业:76,67,80,85,79,81;
![]() 类行业:87,89,76,86,75,84,90,82.
类行业:87,89,76,86,75,84,90,82.
(Ⅰ)计算该城区这三类行业中每类行业的单位个数;
(Ⅱ)若从抽取的![]() 类行业这6个单位中,再随机选取3个单位进行某项调查,求选出的这3个单位中既有“星级”环保单位,又有“非星级”环保单位的概率.
类行业这6个单位中,再随机选取3个单位进行某项调查,求选出的这3个单位中既有“星级”环保单位,又有“非星级”环保单位的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
已知点![]() ,
,![]() ,动点P满足
,动点P满足![]() ,记动点P的轨迹为W.
,记动点P的轨迹为W.
(Ⅰ)求W的方程;
(Ⅱ)直线![]() 与曲线W交于不同的两点C,D,若存在点
与曲线W交于不同的两点C,D,若存在点![]() ,使得
,使得![]() 成立,求实数m的取值范围.
成立,求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com