
分析 (1)根据函数定义域的求法,直接解不等式1≤x2≤3,即可求函数f(x2)的定义域.
(2)根据函数定义域的求法,直接解不等式1≤x+1≤3,1≤2x≤3,即可求函数f(x+1)-f(2x).的定义域.
解答 解:(1)∵函数y=f(x)的定义域为[1,3],
由1≤x2≤3,得:x∈[-$\sqrt{3}$,-1]∪$[1,\sqrt{3}]$,
故函数y=f(x2)的定义域为[-$\sqrt{3}$,-1]∪$[1,\sqrt{3}]$,
(2)函数f(x)的定义域是[1,3],
可得:1≤x+1≤3并且1≤2x≤3,解得:x∈$[\frac{1}{2},\frac{3}{2}]$.
f(x+1)-f(2x)的定义域为:$[\frac{1}{2},\frac{3}{2}]$.
点评 本题主要考查复合函数定义域的求法,直接利用函数f(x)的定义域,解不等式即可.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
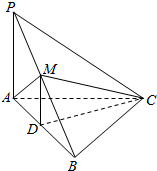 已知三棱锥P-ABC中,PA⊥平面ABC,底面ABC为边长等于3的正三角形,D、M为AB、PB中点,且△PAM为正三角形.
已知三棱锥P-ABC中,PA⊥平面ABC,底面ABC为边长等于3的正三角形,D、M为AB、PB中点,且△PAM为正三角形.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com