
【题目】已知椭圆E: ![]() (a>b>0)的左焦点F1与抛物线y2=﹣4x的焦点重合,椭圆E的离心率为
(a>b>0)的左焦点F1与抛物线y2=﹣4x的焦点重合,椭圆E的离心率为 ![]() ,过点M(m,0)(m>
,过点M(m,0)(m> ![]() )做斜率存在且不为0的直线l,交椭圆E于A,C两点,点P(
)做斜率存在且不为0的直线l,交椭圆E于A,C两点,点P( ![]() ,0),且
,0),且 ![]() 为定值.
为定值.
(1)求椭圆E的方程;
(2)过点M且垂直于l的直线与椭圆E交于B,D两点,求四边形ABCD面积的最小值.
【答案】
(1)
解:抛物线y2=﹣4x的焦点为(﹣1,0),∴F1(1,0),∴c=1,又 ![]() ,a2=b2+c2,
,a2=b2+c2,
解得c=1=b,a2=2.
∴椭圆E的方程为: ![]() +y2=1
+y2=1
(2)
解:设直线l的方程为:ty+m=x,A(x1,y1),C(x2,y2).
联立 ![]() ,化为:(t2+2)y2+2tmy+m2﹣2=0.
,化为:(t2+2)y2+2tmy+m2﹣2=0.
△>0,∴y1+y2= ![]() ,y1y2=
,y1y2= ![]() .
.
![]() =
= ![]() +y1y2=
+y1y2= ![]() +y1y2
+y1y2
= ![]() (y1+y2)+(t2+1)y1y2+
(y1+y2)+(t2+1)y1y2+ ![]()
= ![]()
![]() +(t2+1)
+(t2+1) ![]() +
+ ![]() =
= ![]() 为定值.
为定值.
∴ 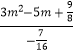 =
= ![]() ,化为:3m2﹣5m+2=0,
,化为:3m2﹣5m+2=0, ![]() ,解得m=1.
,解得m=1.
∴M(1,0).
∴y1+y2= ![]() ,y1y2=
,y1y2= ![]() .
.
∴|AC|= ![]() =
= ![]() =
= ![]() ,
,
把 ![]() 代换t可得:|BD|=
代换t可得:|BD|= ![]() .
.
∴S四边形ABCD= ![]() |AC||BD|=
|AC||BD|= ![]() ×
× ![]() ×
× ![]() =
= ![]() ,
,
令t2+1=k>1,则f(k)= ![]() =
= ![]() =
= ![]() =
= ![]() ≥
≥ ![]() ,
,
当 ![]() =
= ![]() ,即k=2,t=±1时取等号.
,即k=2,t=±1时取等号.
∴四边形ABCD面积的最小值为 ![]()
【解析】(1)抛物线y2=﹣4x的焦点为(﹣1,0),可得c=1,又 ![]() ,a2=b2+c2 , 联立解出即可得出.(2)设直线l的方程为:ty+m=x,A(x1 , y1),C(x2 , y2).与椭圆方程联立化为:(t2+2)y2+2tmy+m2﹣2=0.把根与系数的关系代入
,a2=b2+c2 , 联立解出即可得出.(2)设直线l的方程为:ty+m=x,A(x1 , y1),C(x2 , y2).与椭圆方程联立化为:(t2+2)y2+2tmy+m2﹣2=0.把根与系数的关系代入 ![]() =
= ![]() +y1y2=
+y1y2= ![]() (y1+y2)+(t2+1)y1y2+
(y1+y2)+(t2+1)y1y2+ ![]() =
= ![]() 为定值.可得
为定值.可得 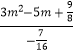 =
= ![]() ,解得m=1.可得|AC|=
,解得m=1.可得|AC|= ![]() = ,把
= ,把 ![]() 代换t可得:|BD|=
代换t可得:|BD|= ![]() .利用S四边形ABCD=
.利用S四边形ABCD= ![]() |AC||BD|与二次函数的单调性即可得出.
|AC||BD|与二次函数的单调性即可得出.


科目:高中数学 来源: 题型:
【题目】若函数y=f(x)的图象上存在两点,使得函数的图象在这两点处的切线互相垂直,则称y=f(x)具有T性质.下列函数中具有T性质的是( )
A.y=sinx
B.y=lnx
C.y=ex
D.y=x3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知过抛物线y2=4x焦点F的直线l交抛物线于A、B两点(点A在第一象限),若 ![]() =3
=3 ![]() ,则直线l的方程为( )
,则直线l的方程为( )
A.x﹣2y﹣1=0
B.2x﹣y﹣2=0
C.x﹣ ![]() y﹣1=0
y﹣1=0
D.![]() x﹣y﹣
x﹣y﹣ ![]() =0
=0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() .
.
(Ⅰ)求函数f(x)的定义域;
(Ⅱ)判定f(x)的奇偶性并证明;
(Ⅲ)用函数单调性定义证明:f(x)在(1,+∞)上是增函数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数f(x)=a(x﹣2)ex+lnx+ ![]() 在(0,2)上存在两个极值点,则a的取值范围为( )
在(0,2)上存在两个极值点,则a的取值范围为( )
A.(﹣∞,﹣ ![]() )
)
B.(﹣ ![]() ,
, ![]() )∪(1,+∞)
)∪(1,+∞)
C.(﹣∞,﹣ ![]() )
)
D.(﹣∞,﹣ ![]() )∪(﹣﹣
)∪(﹣﹣ ![]() ,﹣
,﹣ ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学早上8点开始上课,若学生小典与小方均在![]() 至
至![]() 之间到校,且两人在该时间段的任何时刻到校都是等可能的,则小典比小方至少早5分钟到校的概率为__________.
之间到校,且两人在该时间段的任何时刻到校都是等可能的,则小典比小方至少早5分钟到校的概率为__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com