练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    15．当a为何值时，（a-2）x2+4$\sqrt{5}$x+a-3＜0的解为一切实数．

    分析 根据不等式恒成立，列出关于a的不等式组，求出a的取值范围即可．

    解答 解：不等式，（a-2）x2+4$\sqrt{5}$x+a-3＜0的解为一切实数，
    应满足$\left\{\begin{array}{l}{a-2＜0}\\{△＜0}\end{array}\right.$，
    即$\left\{\begin{array}{l}{a＜2}\\{80-4（a-2）（a-3）＜0}\end{array}\right.$，
    解得$\left\{\begin{array}{l}{a＜2}\\{a＜-2，或a＞7}\end{array}\right.$，
    即a＜-2；
    ∴a的取值范围是{a|a＜-2}．

    点评 本题考查了不等式恒成立的问题，解题的关键是列出满足条件的不等式组，是基础题目．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    5．已知△ABC的三个内角A，B，C所对的边分别为a，b，c，asinC=csinB．
    （Ⅰ）判断△ABC的形状；
    （Ⅱ）若B=30°，a=2，求BC边上中线AD的长．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

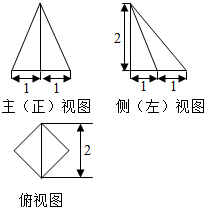    6．已知某棱锥的三视图如图所示，俯视图为正方形，根据图中所给的数据．那么该棱锥的表面积是（　　）
    A．8+4$\sqrt{2}$B．4+2$\sqrt{2}$C．2$\sqrt{2}$+2$\sqrt{3}$D．2+2$\sqrt{2}$+2$\sqrt{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    3．在平面直角坐标系xOy中，已知直线l：x+y+m=0和圆M：x2+y2=9，若圆M上存在点P，使得P到直线l的距离为2，则实数m的取值范围是[-5$\sqrt{2}$，5$\sqrt{2}$]．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．已知函数f（x）=$\left\{\begin{array}{l}{{x}^{2}+ax，x≤1}\\{-x-3，x＞1}\end{array}\right.$，则“a≤-2”是“f（x）在R上单调函数”的（　　）
    A．充分而不必要条件B．必要而不充分条件
    C．充分必要条件D．既不充分也不必要条件

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    20．已知函数f（x）=$\frac{1}{2p}$x2-x+3在区间[-1，2]上的最大值为M，最小值为m，求实数p为何值时，2M+m=3．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    7．已知数列{an}中，a1=a2=1，且对任意的n∈N*，满足an+2=2an+1+an，则a5=17．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    4．记Sn是各项均为正数的等差数列{an}的前n项和，若a1≥1，则（　　）
    A．S2mS2n≥Sm+n2，lnS2mlnS2n≤ln2Sm+n
    B．S2mS2n≤Sm+n2，lnS2mlnS2n≤ln2Sm+n
    C．S2mS2n≥Sm+n2，lnS2mlnS2n≥ln2Sm+n
    D．S2mS2n≤Sm+n2，lnS2mlnS2n≥ln2Sm+n

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    16．设函数f′（x）是函数f（x）（x∈R）的导函数，f（0）=1，且3f（x）=f′（x）-3，则4f（x）＞f′（x）的解集为（　　）
    A．（$\frac{ln4}{3}$，+∞）B．（$\frac{ln2}{3}$，+∞）C．（$\frac{\sqrt{3}}{2}$，+∞）D．（$\frac{\sqrt{e}}{2}$，+∞）

    查看答案和解析>>

    同步练习册答案