
| A. | 0 | B. | 1 | C. | 2 | D. | 4 |
分析 根据一元二次不等式的解集得到a,b满足的条件,利用配方法结合基本不等式进行求解即可.
解答 解:∵二次不等式ax2+2x+b>0解集为{x|x≠-$\frac{1}{a}$},
∴$\left\{\begin{array}{l}{a>0}\\{△=4-4ab=0}\\{-\frac{2}{2a}=-\frac{1}{a}}\end{array}\right.$,则a>0且ab=1,
则a2+b2-a-b=(a+b)2-(a+b)-2ab=(a+b)2-(a+b)-2=(a+b-$\frac{1}{2}$)2-$\frac{9}{4}$,
∵a+b≥2$\sqrt{ab}$=2,∴当a+b=2时,a2+b2-a-b取得最小值此时a2+b2-a-b=22-2-2=0,
故选:A
点评 本题主要考查一元二次不等式以及基本不等式的应用,利用配方法和转化法是解决本题的关键.


 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 物体重量(单位g) | 1 | 2 | 3 | 4 | 5 |
| 弹簧长度(单位cm) | 1.5 | 3 | 4 | 5 | 6.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{125π}{6}$ | B. | $\frac{{125\sqrt{2}π}}{3}$ | C. | $\frac{50π}{3}$ | D. | $\frac{25π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2$\sqrt{37}$-6 | B. | 10-3$\sqrt{5}$ | C. | 8-$\sqrt{37}$ | D. | 2$\sqrt{5}$-2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-2,1] | B. | (-2,1] | C. | [-3,3) | D. | (-2,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
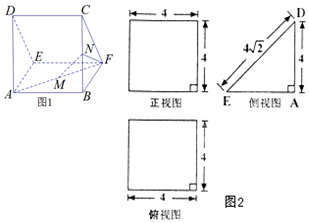 一个多面体的直观图(图1)及三视图(图2)如图所示,其中M、N分别是AF、BC的中点,
一个多面体的直观图(图1)及三视图(图2)如图所示,其中M、N分别是AF、BC的中点,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com