[题目]如图所示.使用纸板可以折叠粘贴制作一个形状为正六棱柱形状的花型锁盒盖的纸盒． (1)求该纸盒的容积,(2)如果有一张长为60cm.宽为40cm的矩形纸板.则利用这张纸板最多可以制作多少个这样的纸盒(纸盒必须用一张纸板制成)．题目和参考答案——青夏教育精英家教网—

【题目】如图所示，使用纸板可以折叠粘贴制作一个形状为正六棱柱形状的花型锁盒盖的纸盒．

（1）求该纸盒的容积；
（2）如果有一张长为60cm，宽为40cm的矩形纸板，则利用这张纸板最多可以制作多少个这样的纸盒（纸盒必须用一张纸板制成）．

【答案】
（1）解：由已知可得：正六棱柱形状的花型锁盒盖的纸盒底面棱长为2cm，高为3cm；

故纸盒的容积V=6× ×22×3=18 cm3

（2）解：由已知可得：制作一个纸盒，需要一张长2×5+0.5=10.5cm，宽3+3+3=9cm的矩形纸，

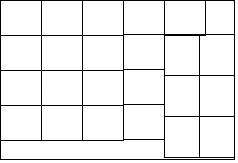
一张长为60cm，宽为40cm的矩形纸板最多可以制作23个这样的纸盒，

如下图所示：

【解析】（1）由已知可得：正六棱柱形状的花型锁盒盖的纸盒底面棱长为2cm，高为3cm；进而可得该纸盒的容积；（2）制作一个纸盒，需要一张长2×5+0.5=10.5cm，宽3+3+3=9cm的矩形纸，进而可得制作方案．
【考点精析】通过灵活运用由三视图求面积、体积，掌握求体积的关键是求出底面积和高；求全面积的关键是求出各个侧面的面积即可以解答此题．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】已知椭圆C的中心在原点，焦点在x轴上，离心率为，过椭圆C上一点P（2，1）作x轴的垂线，垂足为Q．

（Ⅰ）求椭圆C的方程；

（Ⅱ）过点Q的直线l交椭圆C于点A，B，且3+=，求直线l的方程．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知数列{an}满足a1=1，an+1﹣an=2，等比数列{bn}满足b1=a1 ， b4=a4+1．
（1）求数列{an}，{bn}的通项公式；
（2）设cn=an+bn ，求数列{cn}的前n项和Sn ．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】如图：三棱锥P﹣ABC中，PA⊥底面ABC，若底面ABC是边长为2的正三角形，且PB与底面ABC所成的角为．若M是BC的中点，求：

（1）三棱锥P﹣ABC的体积；
（2）异面直线PM与AC所成角的大小（结果用反三角函数值表示）．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】设函数y=f（x）由方程x|x|+y|y|=1确定，下列结论正确的是（请将你认为正确的序号都填上）
·（1）f（x）是R上的单调递减函数；
·（2）对于任意x∈R，f（x）+x＞0恒成立；
·（3）对于任意a∈R，关于x的方程f（x）=a都有解；
·（4）f（x）存在反函数f﹣1（x），且对于任意x∈R，总有f（x）=f﹣1（x）成立．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知数列{an}中，a1=3，a2=5，{an}的前n项和Sn ，且满足Sn+Sn﹣2=2Sn﹣1+2n﹣1（n≥3）．
（1）试求数列{an}的通项公式；
（2）令bn= ，Tn是数列{bn}的前n项和，证明：Tn＜；
（3）证明：对任意给定的m∈（0，），均存在n0∈N+ ，使得当n≥n0时，（2）中的Tn＞m恒成立．