
【题目】已知三棱柱ABC﹣A′B′C′,侧棱与底面垂直,且所有的棱长均为2,E为AA′的中点,F为AB的中点. (Ⅰ)求多面体ABCB′C′E的体积;
(Ⅱ)求异面直线C'E与CF所成角的余弦值.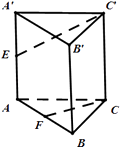
【答案】解:(Ⅰ)直三棱柱ABC﹣A′B′C′的体积V= ![]() =2
=2 ![]() . 三棱锥E﹣A′B′C′的体积V1=
. 三棱锥E﹣A′B′C′的体积V1= ![]() A′E=
A′E= ![]() =
= ![]() .
.
∴多面体ABCB′C′E的体积=V﹣V1= ![]() ;
;
(Ⅱ)如图所示,取A′B′的中点D,连接C′D,DF,DE.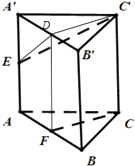
可得四边形CFDC′是矩形.
∴C′D∥CF.
∴∠EC′D即是异面直线C′E与CF所成角.
在Rt△C′DE中,C′D= ![]() ,C′E=
,C′E= ![]() .
.
∴cos∠EC′D= ![]() =
= ![]() =
= ![]() .
.
∴异面直线C′E与CF所成角的余弦值为 ![]() .
.
【解析】(Ⅰ)分别求出直三棱柱ABC﹣A′B′C′的体积V.三棱锥E﹣A′B′C′的体积V1 . 即可得出多面体ABCB′C′E的体积=V﹣V1;(Ⅱ)如图所示,取A′B′的中点D,连接C′D,DF,DE.可得四边形CFDC′是矩形.C′D∥CF.因此∠EC′D即是异面直线C′E与CF所成角.
【考点精析】掌握异面直线及其所成的角是解答本题的根本,需要知道异面直线所成角的求法:1、平移法:在异面直线中的一条直线中选择一特殊点,作另一条的平行线;2、补形法:把空间图形补成熟悉的或完整的几何体,如正方体、平行六面体、长方体等,其目的在于容易发现两条异面直线间的关系.


科目:高中数学 来源: 题型:
【题目】已知圆![]() 经过
经过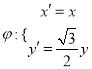 变换后得曲线
变换后得曲线![]() .
.
(1)求![]() 的方程;
的方程;
(2)若![]() 为曲线
为曲线![]() 上两点,
上两点, ![]() 为坐标原点,直线
为坐标原点,直线![]() 的斜率分别为
的斜率分别为![]() 且
且![]() ,求直线
,求直线![]() 被圆
被圆![]() 截得弦长的最大值及此时直线
截得弦长的最大值及此时直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形![]() 是正四棱柱
是正四棱柱![]() 的一个截面,此截面与棱
的一个截面,此截面与棱![]() 交于点
交于点![]() ,
, ![]() ,其中
,其中![]() 分别为棱
分别为棱![]() 上一点.
上一点.
(1)证明:平面![]() 平面
平面![]() ;
;
(2)![]() 为线段
为线段![]() 上一点,若四面体
上一点,若四面体![]() 与四棱锥
与四棱锥![]() 的体积相等,求
的体积相等,求![]() 的长.
的长.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地政府为了对房地产市场进行调控决策,统计部门对外来人口和当地人口进行了买房的心理预期调研,用简单随机抽样的方法抽取了110人进行统计,得到如下列联表(不全):
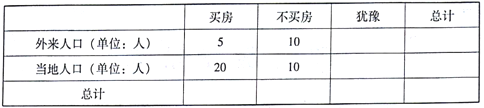
已知样本中外来人口数与当地人口数之比为3:8.
(1)补全上述列联表;
(2)从参与调研的外来人口中用分层抽样方法抽取6人,进一步统计外来人口的某项收入指标,若一个买房人的指标记为3,一个犹豫人的指标记为2,一个不买房人的指标记为1,现在从这6人中再随机选取3人,用![]() 表示这3人指标之和,求
表示这3人指标之和,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2﹣(a+1)x+1(a∈R)
(1)若关于x的不等式f(x)>0的解集为R,求实数a的取值范围;
(2)若关于x的不等式f(x)≤0的解集为P,集合Q={x|0≤x≤1},若P∩Q=,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,四棱锥P﹣ABCD的底面ABCD是边长为1的菱形,∠BCD=60°,E是CD的中点,PA⊥底面ABCD,PA=![]() .
.
(Ⅰ)证明:平面PBE⊥平面PAB;
(Ⅱ)求二面角A﹣BE﹣P的大小.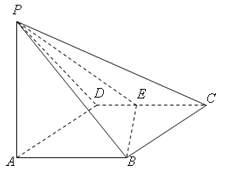
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC﹣A1B1C1中,已知AB⊥侧面BB1C1C,CB⊥C1B,BC=1,CC1=2,A1B1= ![]() ,
, 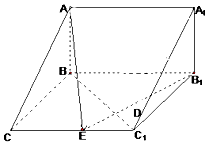
(1)试在棱CC1(不包含端点C,C1)上确定一点E的位置,使得EA⊥EB1;
(2)在(1)的条件下,求AE和BC1所成角.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数f(x),g(x)分别是R上的奇函数、偶函数,且满足f(x)+g(x)=2x , 则有( )
A.f(3)<g(0)<f(4)
B.g(0)<f(4)<f(3)
C.g(0)<f(3)<f(4)
D.f(3)<f(4)<g(0)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com