
【题目】已知函数![]() 在区间[-1,4]上有最大值10和最小值1.设
在区间[-1,4]上有最大值10和最小值1.设![]()
(1)求![]() 的值;
的值;
(2)证明:函数![]() 在
在![]() 上是增函数.
上是增函数.
(3)若不等式![]()
![]() 在
在![]() 上有解,求实数
上有解,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() (2)详见解析(3)
(2)详见解析(3)![]()
【解析】
试题分析:(1)根据函数的对称轴得到关于a的方程组,解出即可;(2)先求出g(x)的表达式,根据定义证明函数的单调性即可;(3)问题转化为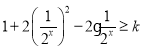 ,令
,令![]() ,则k≤2t2-2t+1,构造新函数,结合函数的单调性从而求出k的范围即可
,则k≤2t2-2t+1,构造新函数,结合函数的单调性从而求出k的范围即可
试题解析:(1)![]()
![]()
因为a>0, 故![]() ,解得
,解得![]() . ……………………4分
. ……………………4分
(2)由已知可得![]() ,设
,设![]() ,
,
∵![]() …………………6分
…………………6分
∵![]() ,∴x1-x2<0,2<x1x2,即x1x2-2>0.
,∴x1-x2<0,2<x1x2,即x1x2-2>0.
∴g(x1)-g(x2)<0,即g(x1)<g(x2).
所以函数g(x)在![]() 上是增函数 ………………………………………8分
上是增函数 ………………………………………8分
(3) ![]() 可化为
可化为![]() ,
,
化为![]() 令
令![]() ,则
,则![]() ……………………10分
……………………10分
因![]() ,故
,故![]()
记![]() 因为
因为![]() ,故
,故![]() ,
,
所以k的取值范围是![]() ………………………………………………………12分
………………………………………………………12分


科目:高中数学 来源: 题型:
【题目】设函数![]() 是定义域为R的奇函数.
是定义域为R的奇函数.
(1)求![]() 的值;
的值;
(2)若![]() ,试判断
,试判断![]() 的单调性(不需证明),并求使不等式
的单调性(不需证明),并求使不等式![]() 恒成立的t的取值范围;
恒成立的t的取值范围;
(3)若![]() ,
,![]() ,求
,求![]() 在
在![]() 上的最小值.
上的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】五一节期间,某商场为吸引顾客消费推出一项优惠活动.活动规则如下:消费额每满100元可转动如图所示的转盘一次,并获得相应金额的返券.(假定指针等可能地停在任一位置, 指针落在区域的边界时,重新转一次)指针所在的区域及对应的返劵金额见右下表.
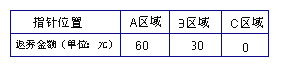

例如:消费218元,可转动转盘2次,所获得的返券金额是两次金额之和.
(1)已知顾客甲消费后获得![]() 次转动转盘的机会,已知他每转一次转盘指针落在区域边界的概率为
次转动转盘的机会,已知他每转一次转盘指针落在区域边界的概率为![]() ,每次转动转盘的结果相互独立,设
,每次转动转盘的结果相互独立,设![]() 为顾客甲转动转盘指针落在区域边界的次数,
为顾客甲转动转盘指针落在区域边界的次数,![]() 的数学期望
的数学期望![]() ,方差
,方差![]() .求
.求![]() 、
、![]() 的值;
的值;
(2)顾客乙消费280元,并按规则参与了活动,他获得返券的金额记为![]() (元).求随机变量
(元).求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】解答下列各题:
(1)在△ABC中,已知C=45°,A=60°,b=2,求此三角形最小边的长及a与B的值;
(2)在△ABC中,已知A=30°,B=120°,b=5,求C及a与c的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法错误的是 ( )
A. 多面体至少有四个面
B. 九棱柱有9条侧棱,9个侧面,侧面为平行四边形
C. 长方体、正方体都是棱柱
D. 三棱柱的侧面为三角形
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了比较两种治疗失眠症的药(分别称为A药,B药)的疗效,随机地选取20位患者服用A药,20位患者服用B药,这40位患者在服用一段时间后,记录他们日平均增加的睡眠时间(单位:h),试验的观测结果如下:
服用A药的20位患者日平均增加的睡眠时间:

服用B药的20位患者日平均增加的睡眠时间:

(Ⅰ)分别计算两组数据的平均数,从计算结果看,哪种药的疗效更好?
(Ⅱ)根据两组数据完成下面茎叶图,从茎叶图看,哪种药的疗效更好?
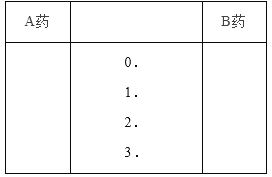
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com