
分析 由题意求出$\overrightarrow{a}•\overrightarrow{b}$,结合(2$\overrightarrow{a}$+λ$\overrightarrow{b}$)•(λ$\overrightarrow{a}$-3$\overrightarrow{b}$)=0,展开后整理求得λ的值.
解答 解:由题意可得$\overrightarrow{a}•\overrightarrow{b}$=$\sqrt{2}$×1×cos45°=1,
再由(2$\overrightarrow{a}$+λ$\overrightarrow{b}$)•(λ$\overrightarrow{a}$-3$\overrightarrow{b}$)=$2λ|\overrightarrow{a}{|}^{2}+({λ}^{2}-6)\overrightarrow{a}•\overrightarrow{b}-3λ|\overrightarrow{b}{|}^{2}=0$,
得$2λ•(\sqrt{2})^{2}+{λ}^{2}-6-3λ=0$,
即λ2+λ-6=0.
解得:λ=-3或λ=2.
点评 本题考查平面向量的数量积运算,考查一元二次方程的解法,属于中档题.


科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2x+y-2016=0 | B. | 2x-y-2016=0 | C. | 2x+y+2016=0 | D. | 2x-y+2016=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
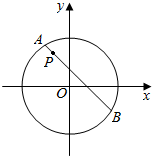 如图,圆O:x2+y2=8内有-点P(-1,2),AB为过P且倾斜角为135°的弦.
如图,圆O:x2+y2=8内有-点P(-1,2),AB为过P且倾斜角为135°的弦.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com