
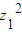 -4z2=16+20i,设这个方程的两个根α、β,满足|α-β|=2
-4z2=16+20i,设这个方程的两个根α、β,满足|α-β|=2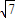 ,求|m|的最大值和最小值.
,求|m|的最大值和最小值. ,首先设出复数m,运用根与系数关系求出α+β及αβ,再借助|α-β|=2
,首先设出复数m,运用根与系数关系求出α+β及αβ,再借助|α-β|=2 找出复数m所满足的关系,根据几何意义求|m|的最大值和最小值.
找出复数m所满足的关系,根据几何意义求|m|的最大值和最小值. ?|α-β|2=28?|(α-β)2|=28?|(α+β)2-4αβ|=28
?|α-β|2=28?|(α-β)2|=28?|(α+β)2-4αβ|=28 ?|(4-a)+(5-b)i|=7?(a-4)2+(b-5)2=72,
?|(4-a)+(5-b)i|=7?(a-4)2+(b-5)2=72, ,最小值为7-
,最小值为7- .
. 列式,转化为复数m的实部和虚部所满足的关系.
列式,转化为复数m的实部和虚部所满足的关系. 

 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案科目:高中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 4 |
| 1 |
| 2 |
| 2 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2-ai |
| a+i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
查看答案和解析>>
科目:高中数学 来源:2012年上海市长宁区高考数学二模试卷(理科)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com