
【题目】在平面直角坐标系![]() 中,已知曲线
中,已知曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).以
为参数).以![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的极坐标方程和曲线
的极坐标方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设动直线![]() :
:![]() 分别与曲线
分别与曲线![]() ,
,![]() 相交于点
相交于点![]() ,
,![]() ,求当
,求当![]() 为何值时,
为何值时,![]() 取最大值,并求
取最大值,并求![]() 的最大值.
的最大值.
【答案】(1)曲线![]() 的极坐标方程是
的极坐标方程是![]() ,曲线
,曲线![]() 的直角坐标方程是
的直角坐标方程是![]() ;(2)当
;(2)当![]() 时,
时,![]() 取最大值,且
取最大值,且![]() .
.
【解析】
(1) 将C1的参数方程消去![]() 可化为普通方程,再利用互化公式
可化为普通方程,再利用互化公式![]() 可得C1的极坐标方程.同理利用互化公式将C2的极坐标方程化为直角坐标方程.
可得C1的极坐标方程.同理利用互化公式将C2的极坐标方程化为直角坐标方程.
(2)法一:将直线的参数方程分别代入曲线![]() 、
、![]() 的普通方程,求得
的普通方程,求得![]() ,利用
,利用![]() 及三角函数的值域可得结果.
及三角函数的值域可得结果.
法二:将![]() (ρ≥0),代入C1, C2的极坐标方程,分别解得:
(ρ≥0),代入C1, C2的极坐标方程,分别解得:![]() .由
.由![]() 结合三角函数的值域可得结果.
结合三角函数的值域可得结果.
(1)曲线![]() 的普通方程为
的普通方程为![]() ,即
,即![]() .将
.将![]() ,
,![]() 代入,
代入,
得![]() ,所以曲线
,所以曲线![]() 的极坐标方程是
的极坐标方程是![]() .
.
由![]() ,得
,得![]() .将
.将![]() ,
,![]() 代入,得
代入,得![]() ,
,
所以曲线![]() 的直角坐标方程是
的直角坐标方程是![]() .
.
(2)解法一:设直线![]() 的倾斜角为
的倾斜角为![]() ,则
,则![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,且
为参数,且![]() ).
).
将![]() 的参数方程代入曲线
的参数方程代入曲线![]() 的普通方程,得
的普通方程,得![]() ,则
,则![]() .
.
将![]() 的参数方程代入曲线
的参数方程代入曲线![]() 的直角坐标方程,得
的直角坐标方程,得![]() ,则
,则![]() .
.
所以![]()
![]() ,
,
据题意,直线![]() 的斜率存在且不为0,则
的斜率存在且不为0,则![]() ,
,
所以当![]() ,即
,即![]() 时,
时,![]() 取最大值,且
取最大值,且![]() .
.
解法二:设直线![]() 的倾斜角为
的倾斜角为![]() ,则
,则![]() 的极坐标方程为
的极坐标方程为![]() .
.
设点![]() ,
,![]() 的极坐标分别为
的极坐标分别为![]() ,
,![]() ,则
,则![]() ,
,![]() .
.
所以![]()
![]() .
.
据题意,直线![]() 的斜率存在且不为0,则
的斜率存在且不为0,则![]() ,
,
所以当![]() ,即
,即![]() 时,
时,![]() 取最大值,且
取最大值,且![]() .
.


科目:高中数学 来源: 题型:
【题目】某种产品的广告费用支出![]() (百万)与销售额
(百万)与销售额![]() (百万)之间有如下的对应数据:
(百万)之间有如下的对应数据:
| 2 | 4 | 5 | 6 | 8 |
| 30 | 40 | 60 | 50 | 70 |
(1)画出散点图;
(2)求回归直线方程;
(3)据此估计广告费用为10(百万)时,销售收入![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a、b、c为△ABC的三个内角A、B、C的对边,向量![]() =(-1,
=(-1,![]() ),
),![]() =(cosA,sinA),若
=(cosA,sinA),若![]() ⊥
⊥![]() ,且acosB+bcosA=csinC,则角B的大小为______.
,且acosB+bcosA=csinC,则角B的大小为______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】箱子里有16张扑克牌:红桃![]() 、
、![]() 、4,黑桃
、4,黑桃![]() 、8、7、4、3、2,草花
、8、7、4、3、2,草花![]() 、
、![]() 、6、5、4,方块
、6、5、4,方块![]() 、5,老师从这16张牌中挑出一张牌来,并把这张牌的点数告诉了学生甲,把这张牌的花色告诉了学生乙,这时,老师问学生甲和学生乙:你们能从已知的点数或花色中推知这张牌是什么牌吗?于是,老师听到了如下的对话:学生甲:我不知道这张牌;学生乙:我知道你不知道这张牌;学生甲:现在我知道这张牌了;学生乙:我也知道了.则这张牌是( )
、5,老师从这16张牌中挑出一张牌来,并把这张牌的点数告诉了学生甲,把这张牌的花色告诉了学生乙,这时,老师问学生甲和学生乙:你们能从已知的点数或花色中推知这张牌是什么牌吗?于是,老师听到了如下的对话:学生甲:我不知道这张牌;学生乙:我知道你不知道这张牌;学生甲:现在我知道这张牌了;学生乙:我也知道了.则这张牌是( )
A. 草花5B. 红桃![]()
C. 红桃4D. 方块5
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在湖南师大附中的校园歌手大赛决赛中,有6位参赛选手(1号至6号)登台演出,由现场的100位同学投票选出最受欢迎的歌手,各位同学须彼此独立地在投票器上选出3位侯选人,其中甲同学是1号选手的同班同学,必选1号,另在2号至6号选手中随机选2名;乙同学不欣赏2号选手,必不选2号,在其他5位选手中随机选出3名;丙同学对6位选手的演唱没有偏爱,因此在1号至6号选手中随机选出3名.
(1)求同学甲选中3号且同学乙未选中3号选手的概率;
(2)设3号选手得到甲、乙、丙三位同学的票数之和为X,求X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,边长为4的正方形ABCD所在平面与正△PAD所在平面互相垂直,M,Q分别为PC,AD的中点.
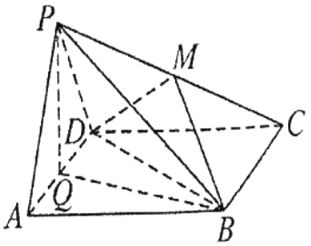
(1)求证:PA//平面MBD.
(2)试问:在线段AB上是否存在一点N,使得平面PCN⊥平面PQB?若存在,试指出点N的位置,并证明你的结论;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右两个焦点分别为
的左、右两个焦点分别为![]() ,P是椭圆上位于第一象限内的点,
,P是椭圆上位于第一象限内的点,![]() 轴,垂足为Q,
轴,垂足为Q,![]() ,
,![]() ,
,![]() 的面积为
的面积为![]() .
.

(1)求椭圆F的方程:
(2)若M是椭圆上的动点,求![]() 的最大值,并求出
的最大值,并求出![]() 取得最大值时M的坐标.
取得最大值时M的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com