
已知函数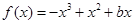 ,
,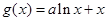 (
(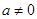 )
)
(1)若函数 存在极值点,求实数b的取值范围;
存在极值点,求实数b的取值范围;
(2)求函数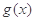 的单调区间;
的单调区间;
(3)当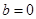 且
且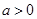 时,令
时,令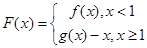 ,
,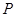 (
(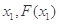 ),
),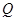 (
(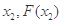 )为曲线y=
)为曲线y=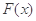 上的两动点,O为坐标原点,能否使得
上的两动点,O为坐标原点,能否使得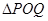 是以O为直角顶点的直角三角形,且斜边中点在y轴上?请说明理由。
是以O为直角顶点的直角三角形,且斜边中点在y轴上?请说明理由。
(1)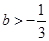
(2)当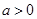 时,
时,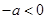 ,函数
,函数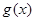 的单调递增区间为
的单调递增区间为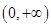 ;
;
当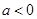 时,
时,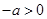 ,函数
,函数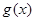 的单调递减区间为
的单调递减区间为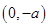 ,单调递增区间为
,单调递增区间为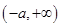 。
。
(3)对任意给定的正实数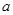 ,曲线上总存在
,曲线上总存在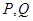 两点,使得
两点,使得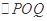 是以O为直角顶点的直角三角形,且斜边中点在y轴上
是以O为直角顶点的直角三角形,且斜边中点在y轴上
解析试题分析:解:(Ⅰ)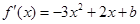 ,若
,若 存在极值点,则
存在极值点,则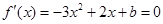 有两个不相等实数根。所以
有两个不相等实数根。所以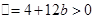 , 2分
, 2分
解得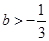 3分
3分
(Ⅱ) 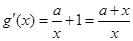 4分
4分
当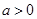 时,
时,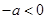 ,函数
,函数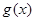 的单调递增区间为
的单调递增区间为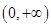 ; 5分
; 5分
当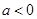 时,
时,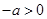 ,函数
,函数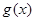 的单调递减区间为
的单调递减区间为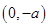 ,单调递增区间为
,单调递增区间为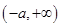 。
。
7分
(Ⅲ) 当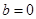 且
且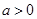 时,
时,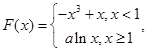 假设使得
假设使得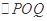 是以O为直角顶点的直角三角形,且斜边中点在y轴上。则
是以O为直角顶点的直角三角形,且斜边中点在y轴上。则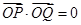 且
且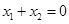 。 8分
。 8分
不妨设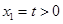 。故
。故 ,则
,则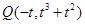 。
。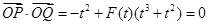 ,
,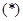 该方程有解 9分
该方程有解 9分
当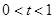 时,则
时,则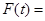
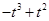 ,代入方程
,代入方程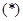 得
得 即
即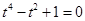 ,而此方程无实数解; 10分
,而此方程无实数解; 10分
当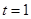 时,
时,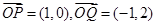 则
则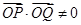 ; 11分
; 11分
当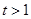 时,则
时,则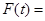
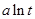 ,代入方程
,代入方程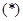 得
得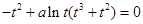 即
即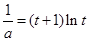 , 12分
, 12分
设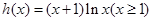 ,则
,则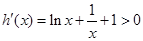 在
在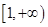 上恒成立。
上恒成立。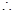
 在
在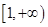 上单调递增,从而
上单调递增,从而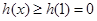 ,则值域为
,则值域为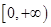 。
。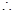 当
当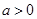 时,方程
时,方程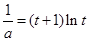 有解,即方程
有解,即方程 有解。 13分
有解。 13分
综上所述,对任意给定的正实数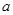 ,曲线上总存在
,曲线上总存在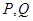 两点,使得
两点,使得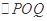 是以O为直角顶点的直角三角形,且斜边中点在y轴上。 14分
是以O为直角顶点的直角三角形,且斜边中点在y轴上。 14分
考点:导数的运用
点评:主要是考查了导数在研究函数单调性以及函数与方程思想的综合运用,属于中档题。


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:高中数学 来源: 题型:解答题
设命题p:函数 的定义域为R;命题q:不等式
的定义域为R;命题q:不等式 对任意
对任意 恒成立.
恒成立.
(Ⅰ)如果p是真命题,求实数 的取值范围;
的取值范围;
(Ⅱ)如果命题“p或q”为真命题且“p且q”为假命题,求实数 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com