
【题目】设函数![]() (
(![]() ,
,![]() 为实数).
为实数).
(1)若![]() 为偶函数,求实数
为偶函数,求实数![]() 的值;
的值;
(2)设![]() ,求函数
,求函数![]() 的最小值(用
的最小值(用![]() 表示).
表示).
科目:高中数学 来源: 题型:
【题目】一幢高楼上安放了一块高约10 米的 LED 广告屏,一测量爱好者在与高楼底部同一水平线上的 C 处测得广告屏顶端A 处的仰角为 31.80°,再向大楼前进 20 米到 D 处,测得广告屏顶端 A 处的仰角为 37.38°(人的高度忽略不计).
(1)求大楼的高度(从地面到广告屏顶端)(精确到 1 米);
(2)若大楼的前方是一片公园空地,空地上可以安放一些长椅,为使坐在其中一个长椅上观看广告屏最清晰(长 椅的高度忽略不计),长椅需安置在距大楼底部 E 处多远?已知视角 ∠AMB( M 为观测者的位置, B 为广告屏 底部)越大,观看得越清晰.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若定义在R上的函数![]() 满足:对于任意实数x、y,总有
满足:对于任意实数x、y,总有![]() 恒成立,我们称
恒成立,我们称![]() 为“类余弦型”函数.
为“类余弦型”函数.
![]() 已知
已知![]() 为“类余弦型”函数,且
为“类余弦型”函数,且![]() ,求
,求![]() 和
和![]() 的值;
的值;
![]() 在
在![]() 的条件下,定义数列
的条件下,定义数列![]() 2,3,
2,3,![]() 求
求![]() 的值.
的值.
![]() 若
若![]() 为“类余弦型”函数,且对于任意非零实数t,总有
为“类余弦型”函数,且对于任意非零实数t,总有![]() ,证明:函数
,证明:函数![]() 为偶函数,设有理数
为偶函数,设有理数![]() ,
,![]() 满足
满足![]() ,判断
,判断![]() 和
和![]() 的大小关系,并证明你的结论.
的大小关系,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某购物商场分别推出支付宝和微信“扫码支付”购物活动,活动设置了一段时间的推广期,由于推广期内优惠力度较大,吸引越来越多的人开始使用“扫码支付”.现统计了活动刚推出一周内每天使用扫码支付的人次,用![]() 表示活动推出的天数,
表示活动推出的天数,![]() 表示每天使用扫码支付的人次,统计数据如下表所示:
表示每天使用扫码支付的人次,统计数据如下表所示:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1)根据散点图判断,在推广期内,扫码支付的人![]() 次关于活动推出天数
次关于活动推出天数![]() 的回归方程适合用
的回归方程适合用![]() 来表示,求出该回归方程,并预测活动推出第
来表示,求出该回归方程,并预测活动推出第![]() 天使用扫码支付的人次;
天使用扫码支付的人次;
(2)推广期结束后,商场对顾客的支付方式进行统计,结果如下表:
支付方式 | 现金 | 会员卡 | 扫码 |
比例 |
|
|
|
商场规定:使用现金支付的顾客无优惠,使用会员卡支付的顾客享受![]() 折优惠,扫码支付的顾客随机优惠,根据统计结果得知,使用扫码支付的顾客,享受
折优惠,扫码支付的顾客随机优惠,根据统计结果得知,使用扫码支付的顾客,享受![]() 折优惠的概率为
折优惠的概率为![]() ,享受
,享受![]() 折优惠的概率为
折优惠的概率为![]() ,享受
,享受![]() 折优惠的概率为
折优惠的概率为![]() .现有一名顾客购买了
.现有一名顾客购买了![]() 元的商品,根据所给数据用事件发生的频率来估计相应事件发生的概率,估计该顾客支付的平均费用是多少?
元的商品,根据所给数据用事件发生的频率来估计相应事件发生的概率,估计该顾客支付的平均费用是多少?
参考数据:设![]() ,
,![]() ,
,![]() ,
,![]()
参考公式:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计公式分别为:
的斜率和截距的最小二乘估计公式分别为: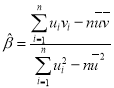 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平面内任意一点![]() 到两定点
到两定点![]() 、
、![]() 的距离之和为
的距离之和为![]() .
.
(1)若点![]() 是第二象限内的一点且满足
是第二象限内的一点且满足![]() ,求点
,求点![]() 的坐标;
的坐标;
(2)设平面内有关于原点对称的两定点![]() ,判别
,判别![]() 是否有最大值和最小值,请说明理由?
是否有最大值和最小值,请说明理由?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正四棱柱ABCD﹣A1B1C1D1中,O是BD的中点,E是棱CC1上任意一点.
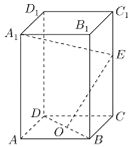
(1)证明:BD⊥A1E;
(2)如果AB=2,![]() ,OE⊥A1E,求AA1的长.
,OE⊥A1E,求AA1的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知各项均为正数的数列![]() 的前
的前![]() 项和为
项和为![]() 且满足:
且满足:![]()
(1)求数列![]() 的通项公式;
的通项公式;
(2)设![]() 求
求![]() 的值;
的值;
(3)是否存在大于2的正整数![]() 使得
使得![]() ?若存在,求出所有符合条件的
?若存在,求出所有符合条件的![]() 若不存在,请说明理由.
若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com