Question

1．已知关于x的不等式x²+2ax+b²≤0的解集为A．
（1）若a是从0，1，2，3四个数中任取的一个数，b是从0，1，2三个数中任取的一个数，求A不为空集的概率；
（2）若a是从区间[0，3]上任取的一个数，b是从区间[0，2]上任取的一个数，求A不为空集的概率．

Answer 1

分析 （1）方程有实根的充要条件为△=（2a）²-4b²≥0，即a²≥b²，由此利用列举法能求出A不为空集的概率．
（2）试验的全部结果构成的区域为{（a，b）|0≤a≤3，0≤b≤2}，满足题意的区域为{（a，b）|0≤a≤3，0≤b≤2，a≥b}，由此利用几何概型能求出A不为空集的概率．

解答 解：（1）方程有实根的充要条件为△=（2a）²-4b²≥0，即a²≥b²，…（1分）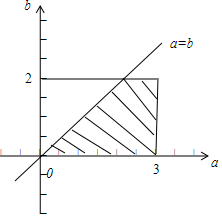
∵a是从0，1，2，3四个数中任取的一个数，b是从0，1，2三个数中任取的一个数，
∴基本事件共有n=4×3=12个，
其中（0，0），（1，0），（1，1），（2，0），（2，1），（2，2），（3，0），（3，1），（3，2）满足条件A不为空集，
∴A不为空集的概率$P=\frac{9}{12}=\frac{3}{4}$．…（5分）
（2）试验的全部结果构成的区域为{（a，b）|0≤a≤3，0≤b≤2}，…（7分）
满足题意的区域为{（a，b）|0≤a≤3，0≤b≤2，a≥b}，…（9分）
所以，A不为空集的概率为$P=\frac{{3×2-\frac{1}{2}×{2^2}}}{3×2}=\frac{2}{3}$．…（10分）

点评 本题考查概率的求法，是中档题，解题时要认真审题，注意列举法和几何概型的合理运用．