
【题目】若![]() 在区间
在区间![]() 上单调递减,则
上单调递减,则![]() 的取值范围为( )
的取值范围为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】A
【解析】分析:由题意,在区间(﹣∞,1]上,a的取值需令真数x2﹣2ax+1+a>0,且函数u=x2﹣2ax+1+a在区间(﹣∞,1]上应单调递减,这样复合函数才能单调递减.
详解:令u=x2﹣2ax+1+a,则f(u)=lgu,
配方得u=x2﹣2ax+1+a=(x﹣a)2 ﹣a2+a+1,故对称轴为x=a,如图所示:
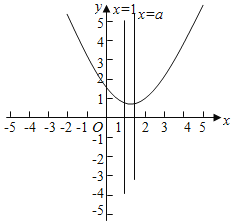
由图象可知,当对称轴a≥1时,u=x2﹣2ax+1+a在区间(﹣∞,1]上单调递减,
又真数x2﹣2ax+1+a>0,二次函数u=x2﹣2ax+1+a在(﹣∞,1]上单调递减,
故只需当x=1时,若x2﹣2ax+1+a>0,
则x∈(﹣∞,1]时,真数x2﹣2ax+1+a>0,
代入x=1解得a<2,所以a的取值范围是[1,2)
故选:A.


科目:高中数学 来源: 题型:
【题目】如图所示,为了测量A,B处岛屿的距离,小明在D处观测,A,B分别在D处的北偏西15°、北偏东45°方向,再往正东方向行驶40海里至C处,观测B在C处的正北方向,A在C处的北偏西60°方向,则A,B两处岛屿间的距离为( ) 
A.![]() 海里
海里
B.![]() 海里
海里
C.![]() 海里
海里
D.40海里
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂要制造A种电子装置45台,B种电子装置55台,需用薄钢板给每台装置配一个外壳,已知薄钢板的面积有两种规格:甲种薄钢板每张面积2m2,可做A、B的外壳分别为3个和5个,乙种薄钢板每张面积3m2,可做A、B的外壳分别为6个和6个,求两种薄钢板各用多少张,才能使总的面积最小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年俄罗斯世界杯激战正酣,某校工会对全校教职工在世界杯期间每天收看比赛的时间作了一次调查,得到如下频数分布表:
收看时间 (单位:小时) |
|
|
|
|
|
|
| 14 |
|
| 28 | 20 | 12 |
(1)若将每天收看比赛转播时间不低于3小时的教职工定义为“球迷”,否则定义为“非球迷”,请根据频数分布表补全![]() 列联表:
列联表:
男 | 女 | 合计 | |
球迷 | 40 | ||
非球迷 |
| ||
合计 |
并判断能否有90%的把握认为该校教职工是否为“球迷”与“性别”有关;
(2)在全校“球迷”中按性别分层抽样抽取6名,再从这6名“球迷”中选取2名世界杯知识讲座.记其中女职工的人数为![]() ,求的
,求的![]() 分布列与数学期望.
分布列与数学期望.
附表及公式:
| 0.15 | 0.10 | 0.05 | 0.025 |
| 2.072 | 2.706 | 3.841 | 5.024 |
![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有同一型号的汽车100辆,为了解这种汽车每耗油![]() 所行路程的情况,现从中随机地抽出10辆,在同一条件下进行耗油
所行路程的情况,现从中随机地抽出10辆,在同一条件下进行耗油![]() 所行路程的试验,得到如下样本数据(单位:km):13.7, 12.7, 14.4, 13.8, 13.3 ,12.5 ,13.5 ,13.6 ,13.1 ,13.4,
所行路程的试验,得到如下样本数据(单位:km):13.7, 12.7, 14.4, 13.8, 13.3 ,12.5 ,13.5 ,13.6 ,13.1 ,13.4,
并分组如下:
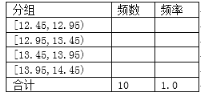
(1)完成上面的频率分布表;
(2)根据上表,在坐标系中画出频率分布直方图.
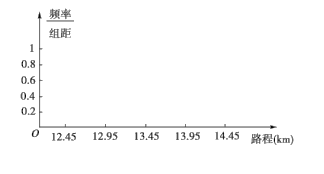
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com