
分析 (1)求出函数的导数,问题转化为$a>\frac{e^x}{x^2}$在$[{\frac{1}{2},1}]$上有解,令$g(x)=\frac{e^x}{x^2}$,故只需$a>g{(x)_{min}},({x∈[{\frac{1}{2},1}]})$,根据函数的单调性求出a的范围即可;
(2)令h(x)=f'(x),则h(x)=ax2-ex,问题转化为方程$2a=\frac{e^x}{x}$有两个根,设φ(x)=$\frac{{e}^{x}}{x}$,根据函数的单调性求出a的范围即可;
(3)求出f′(x1)=${e}^{{x}_{1}}$($\frac{{x}_{1}}{2}$-1),x1∈(0,1),令r(t)=et($\frac{t}{2}$-1),(0<t<1),根据函数的单调性证明即可.
解答 解:因为f'(x)=ax2-bex,所以f'(0)=-b=-1,所以b=1…(1分)
(1)由前可知,f'(x)=ax2-ex
根据题意:f'(x)>0在$[{\frac{1}{2},1}]$上有解,即ax2-ex>0在$[{\frac{1}{2},1}]$上有解 …(2分)
即$a>\frac{e^x}{x^2}$在$[{\frac{1}{2},1}]$上有解,令$g(x)=\frac{e^x}{x^2}$,故只需$a>g{(x)_{min}},({x∈[{\frac{1}{2},1}]})$
所以$g'(x)=\frac{{({x-2}){e^x}}}{x^3}$,所以,当$x∈[{\frac{1}{2},1}]$时,g'(x)<0,所以g(x)在$[{\frac{1}{2},1}]$上单调递减,
所以g(x)min=g(1)=e,所以 a>e…(4分)
(2)令h(x)=f'(x),则h(x)=ax2-ex,所以h'(x)=2ax-ex
由题可知,h'(x)=0有两个根x1,x2,即2ax-ex=0有两个根x1,x2,
又x=0显然不是该方程的根,所以方程$2a=\frac{e^x}{x}$有两个根,…(6分)
设φ(x)=$\frac{{e}^{x}}{x}$,则φ′(x)=$\frac{{e}^{x}(x-1)}{{x}^{2}}$,当x<0时,φ'(x)<0,φ(x)单调递减;
当0<x<1时,φ′(x)<0,φ(x)单调递减;当x>1时,φ′(x)>0,φ(x)单调递增.
故要使方程2a=$\frac{{e}^{x}}{x}$有两个根,只需2a>φ(1)=e,即a>$\frac{e}{2}$,
所以a的取值范围是($\frac{e}{2}$,+∞),
(3)由(2)得:0<x1<1<x2…(9分)
且由h'(x1)=0,得2ax1-${e}^{{x}_{1}}$=0,所以a=$\frac{{e}^{{x}_{1}}}{{2x}_{1}}$,x1∈(0,1)…(10分)
所以f′(x1)=h(x1)=a${{x}_{1}}^{2}$-${e}^{{x}_{1}}$=${e}^{{x}_{1}}$($\frac{{x}_{1}}{2}$-1),x1∈(0,1),
令r(t)=et($\frac{t}{2}$-1),(0<t<1),则r′(t)=et($\frac{t-1}{2}$)<0,
r(t)在(0,1)上单调递减,
所以r(1)<r(t)<r(0),即-$\frac{e}{2}$<f′(x1)<-1.…(12分)
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及转化思想,是一道综合题.


科目:高中数学 来源: 题型:选择题
| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a<c<b | B. | a<b<c | C. | b<a<c | D. | b<c<a |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | 2 | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
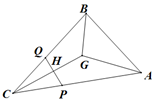 如图,在△ABC中,$\overrightarrow{GA}$+$\overrightarrow{GB}$+$\overrightarrow{GC}$=$\overrightarrow{0}$,$\overrightarrow{CA}$=$\overrightarrow{a}$,$\overrightarrow{CB}$=$\overrightarrow{b}$,已知点P,Q分别为线段CA,CB(不含端点)上的动点,PQ与CG交于H,且H为线段CG中点,若$\overrightarrow{CP}$=m$\overrightarrow{a}$,$\overrightarrow{CQ}$=n$\overrightarrow{b}$,则$\frac{1}{m}$+$\frac{1}{n}$=( )
如图,在△ABC中,$\overrightarrow{GA}$+$\overrightarrow{GB}$+$\overrightarrow{GC}$=$\overrightarrow{0}$,$\overrightarrow{CA}$=$\overrightarrow{a}$,$\overrightarrow{CB}$=$\overrightarrow{b}$,已知点P,Q分别为线段CA,CB(不含端点)上的动点,PQ与CG交于H,且H为线段CG中点,若$\overrightarrow{CP}$=m$\overrightarrow{a}$,$\overrightarrow{CQ}$=n$\overrightarrow{b}$,则$\frac{1}{m}$+$\frac{1}{n}$=( )| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题“若x2-3x+2=0,则 x=1”的逆否命题为:“若x≠1,则x2-3x+2≠0”. | |
| B. | “x=1”是“x2-3x+2=0”的充分必要条件. | |
| C. | 命题p:“?x∈R,sinx+cosx≤$\sqrt{2}$”是真命题 | |
| D. | 若¬(p∧q)为真命题,则p、q至少有一个为假命题. |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $f(x)=x+\frac{1}{x}$ | B. | $f(x)=\frac{1}{x^2}$ | ||
| C. | $f(x)=\sqrt{{x^2}-1}+\sqrt{1-{x^2}}$ | D. | $f(x)=\left\{\begin{array}{l}\frac{1}{2}{x^2}+1,x>0\\-\frac{1}{2}{x^2}-1,x<0\end{array}\right.$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com