
【题目】某商场有奖销售中,购满100元商品得1张奖券,多购多得,1000张奖券为一个开奖单位,设特等奖1个,一等奖10个,二等奖50个.设1张奖券中特等奖、一等奖、二等奖的事件分别为A、B、C,求:
(1)P(A),P(B),P(C);
(2)1张奖券的中奖概率;
(3)1张奖券不中特等奖且不中一等奖的概率.
【答案】(1) ![]() ,
,![]() ,
,![]() .(2)
.(2) ![]() (3)
(3)![]()
【解析】
试题分析:(1)直接代入等可能事件的概率公式![]() 可求;(2)1张奖券的中奖包括三种情况①中特等奖、即事件A发生②中一等奖、即事件B发生③中二等奖、即事件C发生,且AB、C互斥,由互斥事件的概率加法公式可求(3)1张奖券不中特等奖且不中一等奖即为事件
可求;(2)1张奖券的中奖包括三种情况①中特等奖、即事件A发生②中一等奖、即事件B发生③中二等奖、即事件C发生,且AB、C互斥,由互斥事件的概率加法公式可求(3)1张奖券不中特等奖且不中一等奖即为事件![]() ,其对立事件为A+B,利用P(
,其对立事件为A+B,利用P(![]() )=1P(A+B),结合互斥事件的概率公式可求
)=1P(A+B),结合互斥事件的概率公式可求
试题解析:(1)事件A,B,C的概率分别为![]() ,
,![]() ,
,![]() .
.
(2)1张奖券中奖包含中特等奖、一等奖、二等奖.设“1张奖券中奖”这个事件为M,则M=A+B+C. ∵A、B、C两两互斥,
∴P(M)=P(A+B+C)=P(A)+P(B)+P(C)=![]()
故1张奖券的中奖概率为![]() .
.
(3)设“1张奖券不中特等奖且不中一等奖”为事件N,则事件N与“1张奖券中特等奖或中一等奖”为对立事件,
∴P(N)=1-P(A+B)=1-(![]() +
+![]() )=
)=![]() .
.
故1张奖券不中特等奖且不中一等奖的概率为![]() .
.


科目:高中数学 来源: 题型:
【题目】城市公交车的数量若太多则容易造成资源的浪费;若太少又难以满足乘客需求.某市公交公司在某站台的60名候车乘客中随机抽取15人,将他们的候车时间作为样本分成5组,如下表所示(单位:分钟):
组别 | 候车时间 | 人数 |
一 |
| 2 |
二 |
| 6 |
三 |
| 4 |
四 |
| 2 |
五 |
| 1 |
(1)估计这60名乘客中候车时间少于10分钟的人数;
(2)若从上表第三、四组的6人中任选2人作进一步的调查,求抽到的两人恰好来自不同组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学为了了解全校学生的上网情况,在全校采用随机抽样的方法抽取了40名学生(其中男女生人数恰好各占一半)进行问卷调查,并进行了统计,按男女分为两组,再将每组学生的月上网次数分为5组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,得到如图所示的频率分布直方图:
,得到如图所示的频率分布直方图:
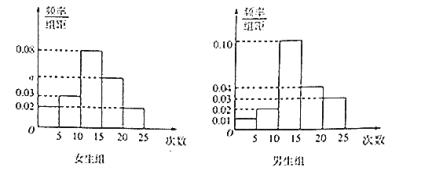
(Ⅰ)写出![]() 的值;
的值;
(Ⅱ)在抽取的40名学生中,从月上网次数不少于20次的学生中随机抽取3人 ,并用![]() 表示其中男生的人数,求
表示其中男生的人数,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的两个焦点与短轴的一个端点是等边三角形的三个顶点,且长轴长为4.
的两个焦点与短轴的一个端点是等边三角形的三个顶点,且长轴长为4.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)若![]() 是椭圆
是椭圆![]() 的左顶点,经过左焦点
的左顶点,经过左焦点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,求
两点,求![]() 与
与![]() 的面积之差的绝对值的最大值.(
的面积之差的绝对值的最大值.(![]() 为坐标原点)
为坐标原点)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的两个焦点与短轴的一个端点是等边三角形的三个顶点,且长轴长为4.
的两个焦点与短轴的一个端点是等边三角形的三个顶点,且长轴长为4.
(1)求椭圆![]() 的方程;
的方程;
(2)若![]() 是椭圆
是椭圆![]() 的左顶点,经过左焦点
的左顶点,经过左焦点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,求
两点,求![]() 与
与![]() 的面积之差的绝对值的最大值.(
的面积之差的绝对值的最大值.(![]() 为坐标原点)
为坐标原点)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com