
【题目】如图,直三棱柱ABCA1B1C1中(侧棱与底面垂直的棱柱),AC=BC=1,∠ACB=90°,AA1=![]() ,D 是A1B1的中点.
,D 是A1B1的中点.
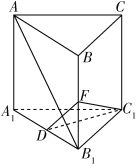
(1)求证:C1D⊥平面AA1B1B;
(2)当点F 在BB1上的什么位置时,AB1⊥平面C1DF ?并证明你的结论.
【答案】(1)见解析;(2)见解析
【解析】
(1)由![]() 是直三棱柱,D是A1B1的中点和题设条件,得C1D⊥A1B1和AA1⊥C1D,利用线面垂直的判定定理,即可证明;
是直三棱柱,D是A1B1的中点和题设条件,得C1D⊥A1B1和AA1⊥C1D,利用线面垂直的判定定理,即可证明;
(2)作![]() 交AB1于点E,延长DE交BB1于点F,连接C1F,则AB1⊥平面C1DF,点F即所求.
交AB1于点E,延长DE交BB1于点F,连接C1F,则AB1⊥平面C1DF,点F即所求.
(1)∵![]() 是直三棱柱,
是直三棱柱,
∴A1C1=B1C1=1,且∠A1C1B1=90°.
又D是A1B1的中点,
∴C1D⊥A1B1.
∵AA1⊥平面A1B1C1,C1D ![]() 平面A1B1C1,
平面A1B1C1,
∴AA1⊥C1D,
∴C1D⊥平面![]() .
.
(2)作![]() 交AB1于点E,延长DE交BB1于点F,连接C1F,则AB1⊥平面C1DF,点F即所求.
交AB1于点E,延长DE交BB1于点F,连接C1F,则AB1⊥平面C1DF,点F即所求.
事实上,∵C1D⊥平面AA1B1B,AB1![]() 平面AA1B1B,
平面AA1B1B,
∴C1D⊥AB1.
又AB1⊥DF,![]() ,
,
∴AB1⊥平面C1DF.
∵AA1=A1B1=![]() ,
,
∴四边形AA1B1B为正方形.
又D为A1B1的中点,DF⊥AB1,
∴F为BB1的中点,
∴当点F为BB1的中点时,AB1⊥平面C1DF.


科目:高中数学 来源: 题型:
【题目】圆周上有![]() 个点
个点![]() ,用弦两两连结起来,其中任何3条弦都不在圆内共点.现将由此形成的互补重叠的圆内区域的个数记为
,用弦两两连结起来,其中任何3条弦都不在圆内共点.现将由此形成的互补重叠的圆内区域的个数记为![]() .
.
(1).直接画图求出![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ;
;
(2).确定![]() 的表达式.
的表达式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 为一个56元集合.求最小的正整数
为一个56元集合.求最小的正整数![]() ,使得对集合
,使得对集合![]() 的任意15个子集,只要它们中间任何七个的并的元素个数均不少于
的任意15个子集,只要它们中间任何七个的并的元素个数均不少于![]() ,则这15个子集中一定存在三个集合,使得它们的交集非空.
,则这15个子集中一定存在三个集合,使得它们的交集非空.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某人在微信群中发了一个8元“拼手气”红包,被甲、乙、丙三人抢完,若三人均领到整数元,且每人至少领到1元,则甲领到的钱数不少于其他任何人的概率为
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
以平面直角坐标系![]() 的原点为极点,
的原点为极点, ![]() 轴的正半轴为极轴,建立极坐标系,两种坐标系中取相同的长度单位,直线
轴的正半轴为极轴,建立极坐标系,两种坐标系中取相同的长度单位,直线![]() 的参数方程为
的参数方程为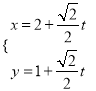 ,圆
,圆![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程与圆
的普通方程与圆![]() 的直角坐标方程;
的直角坐标方程;
(2)设曲线![]() 与直线
与直线![]() 交于
交于![]() 两点,若
两点,若![]() 点的直角坐标为
点的直角坐标为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学高三年级从甲、乙两个班级各选出7名学生参加数学基本公式大赛,他们取得的成绩(满分100分)的茎叶图如图,其中甲班学生的平均分是85,乙班学生成绩的中位数是83.
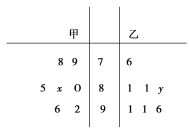
(1)求x和y的值;
(2)从成绩在90分以上的学生中随机抽取两名学生,求甲班至少有一名学生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设整数![]() ,对置于
,对置于![]() 个点
个点![]() 及点
及点![]() 处的卡片作如下操作:操作
处的卡片作如下操作:操作![]() :若某个点
:若某个点![]() 处的卡片数不少于3,则可从中取出三张,在三点
处的卡片数不少于3,则可从中取出三张,在三点![]() 、
、![]() 、
、![]() 处各放一张
处各放一张![]() ;操作
;操作![]() :若点
:若点![]() 处的卡片数不少于
处的卡片数不少于![]() ,则可从中取出
,则可从中取出![]() 张,在
张,在![]() 个点
个点![]() 处各放一张。证明:只要放置于这
处各放一张。证明:只要放置于这![]() 个点处的卡片总数不少于
个点处的卡片总数不少于![]() ,则总能通过若干次操作,使得每个点处的卡片数均不少于
,则总能通过若干次操作,使得每个点处的卡片数均不少于![]() 。
。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com