
【题目】某工厂对一批新产品的长度(单位:![]() )进行检测,如下图是检测结果的频率分布直方图,据此估计这批产品的中位数与平均数分别为( )
)进行检测,如下图是检测结果的频率分布直方图,据此估计这批产品的中位数与平均数分别为( )

A.20,22.5B.22.5,25C.22.5,22.75D.22.75,22.75
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图,梯形ABCD内接于⊙O,AD∥BC,过点C作⊙O的切线,交BD的延长线于点P,交AD的延长线于点E. 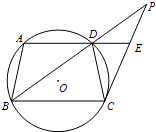
(1)求证:AB2=DEBC;
(2)若BD=9,AB=6,BC=9,求切线PC的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂为了对新研发的一种产品进行合理定价,将该产品按事先拟定的价格进行试销,得到如下数据:

(1)求回归直线方程![]() ,其中
,其中![]() ,
,![]() .
.
(2)预计在今后的销售中,销量与单价仍然服从(1)中的关系,且该产品的成本是4元/件,为使工厂获得最大利润,该产品的单价应定为多少元?(利润=销售收入-成本)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数学40名数学教师,按年龄从小到大编号为1,2,…40。现从中任意选取6人分成两组分配到A,B两所学校从事支教工作,其中三名编号较小的教师在一组,三名编号较大的教师在另一组,那么编号为8,12,28的数学教师同时入选并被分配到同一所学校的方法种数是
A. 220 B. 440 C. 255 D. 510
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司新上一条生产线,为保证新的生产线正常工作,需对该生产线进行检测,现从该生产线上随机抽取100件产品,测量产品数据,用统计方法得到样本的平均数![]() ,标准差
,标准差![]() ,绘制如图所示的频率分布直方图,以频率值作为概率估值。
,绘制如图所示的频率分布直方图,以频率值作为概率估值。

(1)从该生产线加工的产品中任意抽取一件,记其数据为![]() ,依据以下不等式评判(
,依据以下不等式评判(![]() 表示对应事件的概率)
表示对应事件的概率)
①![]()
②![]()
③![]()
评判规则为:若至少满足以上两个不等式,则生产状况为优,无需检修;否则需检修生产线,试判断该生产线是否需要检修;
(2)将数据不在![]() 内的产品视为次品,从该生产线加工的产品中任意抽取2件,次品数记为
内的产品视为次品,从该生产线加工的产品中任意抽取2件,次品数记为![]() ,求
,求![]() 的分布列与数学期望
的分布列与数学期望![]() 。
。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】微信红包是一款年轻人非常喜欢的手机应用.某网络运营商对甲、乙两个品牌各![]() 种型号的手机在相同环境下抢到红包的个数进行统计,得到如下数据:
种型号的手机在相同环境下抢到红包的个数进行统计,得到如下数据:
品牌 型号 | Ⅰ | Ⅱ | Ⅲ | Ⅳ | Ⅴ |
甲品牌(个) | 4 | 3 | 8 | 6 | 12 |
乙品牌(个) | 5 | 7 | 9 | 4 | 3 |
红包个数 手机品牌 | 优良 | 一般 | 合计 |
甲品牌(个) | |||
乙品牌(个) | |||
合计 |
(Ⅰ)如果抢到红包个数超过![]() 个的手机型号为“优良”,否则为“一般”,请完成上述表格,并据此判断是否有
个的手机型号为“优良”,否则为“一般”,请完成上述表格,并据此判断是否有![]() 的把握认为抢到红包的个数与手机品牌有关?
的把握认为抢到红包的个数与手机品牌有关?
(Ⅱ)不考虑其它因素,现要从甲、乙两品牌的![]() 种型号中各选出
种型号中各选出![]() 种型号的手机进行促销活动,求恰有一种型号是“优良”,另一种型号是“一般”的概率;
种型号的手机进行促销活动,求恰有一种型号是“优良”,另一种型号是“一般”的概率;
参考公式:随机变量![]() 的观察值计算公式:
的观察值计算公式:![]() ,
,
其中![]() .临界值表:
.临界值表:
| 0.10 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知极点与直角坐标系的原点重合,极轴与x轴的正半轴重合,圆C的极坐标方程是ρ=asinθ,直线l的参数方程是 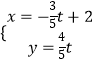 (t为参数)
(t为参数)
(1)若a=2,直线l与x轴的交点是M,N是圆C上一动点,求|MN|的最大值;
(2)直线l被圆C截得的弦长等于圆C的半径的 ![]() 倍,求a的值.
倍,求a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() ,
,![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的单调区间;
的单调区间;
(2)当![]() 时,若函数
时,若函数![]() 在区间
在区间![]() 上的最小值是
上的最小值是![]() ,求
,求![]() 的值;
的值;
(3)设![]() ,
,![]() 是函数
是函数![]() 图象上任意不同的两点,线段
图象上任意不同的两点,线段![]() 的中点为
的中点为![]() ,直线
,直线![]() 的斜率为
的斜率为![]() .证明:
.证明:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某届奥运会上,中国队以26金18银26铜的成绩称金牌榜第三、奖牌榜第二,某校体育爱好者在高三年级一班至六班进行了“本届奥运会中国队表现”的满意度调查![]() 结果只有“满意”和“不满意”两种
结果只有“满意”和“不满意”两种![]() ,从被调查的学生中随机抽取了50人,具体的调查结果如表:
,从被调查的学生中随机抽取了50人,具体的调查结果如表:
班号 | 一班 | 二班 | 三班 | 四班 | 五班 | 六班 |
频数 | 5 | 9 | 11 | 9 | 7 | 9 |
满意人数 | 4 | 7 | 8 | 5 | 6 | 6 |
(1)在高三年级全体学生中随机抽取一名学生,由以上统计数据估计该生持满意态度的概率;
(2)若从一班至二班的调查对象中随机选取4人进行追踪调查,记选中的4人中对“本届奥运会中国队表现”不满意的人数为![]() ,求随机变量
,求随机变量![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com