
���� �⣺��������f��x��=$\left\{\begin{array}{l}{sinx��sinx��cosx}\\{cosx��sinx��cosx}\end{array}\right.$��ͼ�����ν�Ͽɵý��ۣ�
��� �⣺�ߺ���f��x��=$\left\{\begin{array}{l}{sinx��sinx��cosx}\\{cosx��sinx��cosx}\end{array}\right.$����ʾȡsinx��cosx��ֵ��С�ģ�����ͼ����ͼ�к�ɫ������ʾ��
��sinx��cosx��������Ϊ2�еĺ�������f��x������С������Ϊ2�У��ʢ���ȷ��
���f��x����ͼ��ɵ�f��x�������ֵΪ1����СֵΪ-$\frac{\sqrt{2}}{2}$���ʢڴ���
���f��x����ͼ��ɵ�f��x������СֵΪ-$\frac{\sqrt{2}}{2}$��f��x����ͼ��ĶԳ���Ϊֱ��$x=k��+\frac{��}{4}��{k��Z}��$��
�ʢ���ȷ���ܴ���
����f��x����$[{\frac{��}{2}����}]$�ϵ����ݼ����ʢ���ȷ��
�ʴ�Ϊ���٢ۢݣ�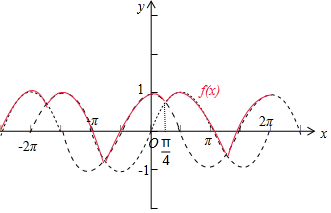
���� ������Ҫ�������Ǻ�����ͼ������ʣ������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2x+6 | B�� | 6x-2 | C�� | 3x-1 | D�� | x+3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �ཻ | B�� | ���� | C�� | ���� | D�� | ��ȷ�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-�ޣ�2] | B�� | ��-�ޣ�2�� | C�� | ��4��+�ޣ� | D�� | [4��+�ޣ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com