
| x | -8 | -4 | 3 | 5 |
| y | 19 | 7 | -3 | -9 |
| A. | $\frac{3}{2}$ | B. | -$\frac{3}{2}$ | C. | $\frac{2}{3}$ | D. | -$\frac{2}{3}$ |
分析 求出横标和纵标的平均数,写出样本中心点,把样本中心点代入线性回归方程,得到关于a的方程,解方程即可.
解答 解:∵$\overline{x}$=$\frac{-8-4+3+5}{4}$=-1,$\overline{y}$=$\frac{19+7-3-9}{4}$=$\frac{7}{2}$,
∴这组数据的样本中心点是(-1,$\frac{7}{2}$)
把样本中心点代入回归直线方程$\stackrel{∧}{y}$=-2x+$\stackrel{∧}{a}$
∴$\frac{7}{2}$=2+a,
∴a=$\frac{3}{2}$
故选:A.
点评 本题考查线性回归方程,解题的关键是线性回归直线一定过样本中心点,这是求解线性回归方程的步骤之一.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
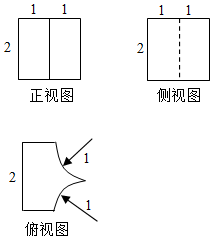 一个几何体的三视图如图所示,其中俯视图曲线部分是两个半径为1的圆弧,则这个几何体的体积是( )
一个几何体的三视图如图所示,其中俯视图曲线部分是两个半径为1的圆弧,则这个几何体的体积是( )| A. | 8-$\frac{π}{4}$ | B. | 8-$\frac{π}{2}$ | C. | 8-π | D. | 8-2π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -4 | B. | -3 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
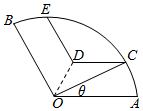 如图,扇形AOB是一个植物园的平面示意图,其中∠AOB=$\frac{2π}{3}$,半径OA=OB=1km,为了便于游客观赏,拟在圆内铺设一条从入口A到出口B的观赏道路,道路由弧$\widehat{AC}$,线段CD,线段DE和弧$\widehat{EB}$组成,且满足:$\widehat{AC}$=$\widehat{EB}$,CD∥AO.DE∥OB,OD∈[$\frac{\sqrt{3}}{3}$,$\frac{\sqrt{6}}{3}$](单位:km),设∠AOC=θ.
如图,扇形AOB是一个植物园的平面示意图,其中∠AOB=$\frac{2π}{3}$,半径OA=OB=1km,为了便于游客观赏,拟在圆内铺设一条从入口A到出口B的观赏道路,道路由弧$\widehat{AC}$,线段CD,线段DE和弧$\widehat{EB}$组成,且满足:$\widehat{AC}$=$\widehat{EB}$,CD∥AO.DE∥OB,OD∈[$\frac{\sqrt{3}}{3}$,$\frac{\sqrt{6}}{3}$](单位:km),设∠AOC=θ.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com