
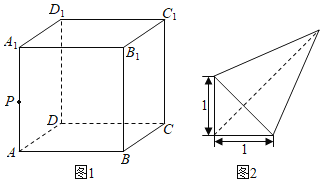
【题目】如图1,已知正方体![]() 的棱长为
的棱长为![]() ,
,![]() 为棱
为棱![]() 的中点,
的中点,![]() 分别是线段
分别是线段![]() ,
,![]() ,
,![]() 上的点,若三棱锥
上的点,若三棱锥![]() 的俯视图如图2,则三棱锥
的俯视图如图2,则三棱锥![]() 的体积最大值为( )
的体积最大值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】D
【解析】
通过俯视图可确定M,Q为所在棱中点,由线面关系可确定当N与C重合时,N到平面PQM的距离最大.由截面图形ACC1A1中的线线关系可知CE,再求出三角形PQM的面积,代入棱锥体积公式求解.
由俯视图知,M为A1D1的中点,Q为A1B1的中点,N为CC1上任意一点,
如图1所示:由中位线可知:PQ∥AB1,MP∥AD1,且![]() ,
,![]() ,
,
∴平面PMQ∥平面AB1D1,由正方体中线面关系可知:A1C⊥平面AB1D1,∴A1C⊥平面PMQ,
∴当N与C重合,点N到平面PMQ的距离最大,截面ACC1A1如图2所示,其中平面ACC1A1∩平面PMQ=PS,
平面ACC1A1∩平面AB1D1=AT,则![]() ,∴CE=
,∴CE=![]() ,
,
又A1C=![]() ,∴最大值为CE=
,∴最大值为CE=![]() A1C=
A1C=![]() =
=![]() .
.
又![]() ,∴三棱锥P﹣MNQ的体积最大值为
,∴三棱锥P﹣MNQ的体积最大值为![]() .
.
故选:D.
图1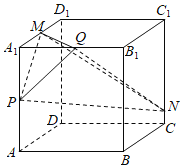 图2
图2 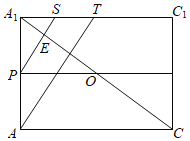


 学习实践园地系列答案
学习实践园地系列答案科目:高中数学 来源: 题型:
【题目】某险种的基本保费为a(单位:元),继续购买该险种的投保人称为续保人,续保人本年度的保费与其上年度出险次数的关联如下:
上年度出险次数 | 0 | 1 | 2 | 3 | 4 | ≥5 |
保费 | 0.85a | a | 1.25a | 1.5a | 1.75a | 2a |
随机调查了该险种的200名续保人在一年内的出险情况,得到如下统计表:
出险次数 | 0 | 1 | 2 | 3 | 4 | ≥5 |
频数 | 60 | 50 | 30 | 30 | 20 | 10 |
(1)记A为事件:“一续保人本年度的保费不高于基本保费”,求P(A)的估计值;
(2)记B为事件:“一续保人本年度的保费高于基本保费但不高于基本保费的160%”,求P(B)的估计值;
(3)求续保人本年度平均保费的估计值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,BC边上的高所在直线的方程为x-2y+1=0,∠A的平分线所在的直线方程为y=0.若点B的坐标为(1,2),求点A和点C的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为调查某地区老年人是否需要志愿者提供帮助,用简单随机抽样的方法从该地区调查了500位老年人,结果如下:
性别 是否需要志愿者 | 男 | 女 |
需要 | 40 | 30 |
不需要 | 160 | 270 |
附:![]() 的观测值
的观测值
| 0.05 | 0.01 | 0.001 |
| 3.841 | 6.635 | 10.828 |
(1)估计该地区老年人中,需要志愿者提供帮助的老年人的比例;
(2)在犯错误的概率不超过0.01的前提下是否可认为该地区的老年人是否需要志愿者提供帮助与性别有关?
查看答案和解析>>
科目:高中数学 来源: 题型:
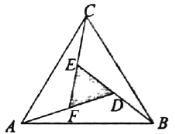
【题目】赵爽是我国古代数学家、天文学家,大约在公元222年,赵爽为《周髀算经》一书作序时,介绍了“勾股圆方图”,亦称“赵爽弦图”(以弦为边长得到的正方形是由4个全等的直角三角形再加上中间的一个小正方形组成).类比“赵爽弦图”,可类似地构造如图所示的图形,它是由3个全等的三角形与中间的一个小等边三角形拼成的一个大等边三角形,设![]() ,若在大等边三角形中随机取一点,则此点取自小等边三角形的概率是( ).
,若在大等边三角形中随机取一点,则此点取自小等边三角形的概率是( ).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从分别写有数字1,2,3,4,5的5张卡片中随机抽取1张,放回后再随机抽取1张,则抽得的第一张卡片上的数字不大于第二张卡片的概率是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() (
(![]() )的离心率为
)的离心率为![]() ,且经过点
,且经过点![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 作直线
作直线![]() 与椭圆
与椭圆![]() 交于不同的两点
交于不同的两点![]() ,
,![]() ,试问在
,试问在![]() 轴上是否存在定点
轴上是否存在定点![]() 使得直线
使得直线![]() 与直线
与直线![]() 恰关于
恰关于![]() 轴对称?若存在,求出点
轴对称?若存在,求出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中
,其中![]() .
.
(1)若曲线![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() ,求函数
,求函数![]() 的解析式;
的解析式;
(2)讨论函数![]() 的单调性;
的单调性;
(3)若对于任意的![]() ,不等式
,不等式![]() 在
在![]() 上恒成立,求
上恒成立,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对年利率为![]() 的连续复利,要在
的连续复利,要在![]() 年后达到本利和
年后达到本利和![]() ,则现在投资值为
,则现在投资值为![]() ,
,![]() 是自然对数的底数.如果项目
是自然对数的底数.如果项目![]() 的投资年利率为
的投资年利率为![]() 的连续复利.
的连续复利.
(1)现在投资5万元,写出满![]() 年的本利和,并求满10年的本利和;(精确到0.1万元)
年的本利和,并求满10年的本利和;(精确到0.1万元)
(2)一个家庭为刚出生的孩子设立创业基金,若每年初一次性给项目![]() 投资2万元,那么,至少满多少年基金共有本利和超过一百万元?(精确到1年)
投资2万元,那么,至少满多少年基金共有本利和超过一百万元?(精确到1年)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com