
【题目】已知数列![]() 的首项a1=1,前n项和为Sn.设λ与k是常数,若对一切正整数n,均有
的首项a1=1,前n项和为Sn.设λ与k是常数,若对一切正整数n,均有![]() 成立,则称此数列为“λ~k”数列.
成立,则称此数列为“λ~k”数列.
(1)若等差数列![]() 是“λ~1”数列,求λ的值;
是“λ~1”数列,求λ的值;
(2)若数列![]() 是“
是“![]() ”数列,且an>0,求数列
”数列,且an>0,求数列![]() 的通项公式;
的通项公式;
(3)对于给定的λ,是否存在三个不同的数列![]() 为“λ~3”数列,且an≥0?若存在,求λ的取值范围;若不存在,说明理由,
为“λ~3”数列,且an≥0?若存在,求λ的取值范围;若不存在,说明理由,
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:高中数学 来源: 题型:
【题目】某公司对旗下的甲、乙两个门店在1至9月份的营业额(单位:万元)进行统计并得到如图折线图.

下面关于两个门店营业额的分析中,错误的是( )
A.甲门店的营业额折线图具有较好的对称性,故而营业额的平均值约为32万元
B.根据甲门店的营业额折线图可知,该门店营业额的平均值在[20,25]内
C.根据乙门店的营业额折线图可知,其营业额总体是上升趋势
D.乙门店在这9个月份中的营业额的极差为25万元
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】十九大提出:坚决打赢脱贫攻坚战,做到精准扶贫.某县积极引导农民种植一种名贵中药材,从而大大提升了该县村民的经济收入.2019年年底,该机构从该县种植的这种名贵药材的农户中随机抽取了100户,统计了他们2019年因种植,中药材所获纯利润(单位:万元)的情况(假定农户因种植中药材这一项一年最多获利11万元),统计结果如下表所示:
![]()
(1)由表可以认为,该县农户种植中药材所获纯利润Z(单位:万元)近似地服从正态分布![]() ,其中
,其中![]() 近似为样本平均数
近似为样本平均数![]() (每组数据取区间的中点值),
(每组数据取区间的中点值),![]() 近似为样本方差
近似为样本方差![]() .若该县有1万户农户种植了该中药材,试估算所获纯利润Z在区间(1.9,8.2)的户数;
.若该县有1万户农户种植了该中药材,试估算所获纯利润Z在区间(1.9,8.2)的户数;
(2)为答谢广大农户的积极参与,该调查机构针对参与调查的农户举行了抽奖活动,抽奖规则如下:在一箱子中放置5个除颜色外完全相同的小球,其中红球1个,黑球4个.让农户从箱子中随机取出一个小球,若取到红球,则抽奖结束;若取到黑球,则将黑球放回箱中,让他继续取球,直到取到红球为止(取球次数不超过10次).若农户取到红球,则视为中奖,获得2000元的奖励,若一直未取到红球,则视为不中奖.现农户张明参加了抽奖活动,记他中奖时取球的次数为随机变量X,他取球的次数为随机变量Y.
①证明:![]() 为等比数列;
为等比数列;
②求Y的数学期望.(精确到0.001)
参考数据:![]() .若随机变量
.若随机变量![]() 则
则![]()
![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年春节突如其来的新型冠状病毒肺炎在湖北爆发,一方有难八方支援,全国各地的白衣天使走上战场的第一线,某医院抽调甲、乙两名医生,抽调![]() 、
、![]() 、
、![]() 三名护士支援武汉第一医院与第二医院,参加武汉疫情狙击战其中选一名护士与一名医生去第一医院,其它都在第二医院工作,则医生甲和护士
三名护士支援武汉第一医院与第二医院,参加武汉疫情狙击战其中选一名护士与一名医生去第一医院,其它都在第二医院工作,则医生甲和护士![]() 被选在第一医院工作的概率为( )
被选在第一医院工作的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为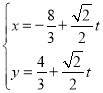 (
(![]() 为参数).以坐标原点
为参数).以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,其中
,其中![]() .
.
(Ⅰ)写出直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)在平面直角坐标系![]() 中,设直线
中,设直线![]() 与曲线
与曲线![]() 相交于
相交于![]() ,
,![]() 两点.若点
两点.若点![]() 恰为线段
恰为线段![]() 的三等分点,求
的三等分点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校课外兴趣小组利用假期到植物园开展社会实践活动,研究某种植物生长情况与温度的关系.现收集了该种植物月生长量y(cm)与月平均气温x(℃)的8组数据,并制成如图所示的散点图.
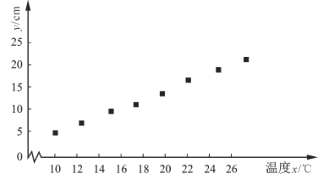
根据收集到的数据,计算得到如下值:
|
|
|
|
18 | 12.325 | 224.04 | 235.96 |
(1)求出y关于x的线性回归方程(最终结果的系数精确到0.01),并求温度为28℃时月生长量y的预报值;
(2)根据y关于x的回归方程,得到残差图如图所示,分析该回归方程的拟合效果.

附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】共享单车又称为小黄车,近年来逐渐走进了人们的生活,也成为减少空气污染,缓解城市交通压力的一种重要手段.为调查某地区居民对共享单车的使用情况,从该地区居民中按年龄用随机抽样的方式随机抽取了![]() 人进行问卷调查,得到这
人进行问卷调查,得到这![]() 人对共享单车的评价得分统计填入茎叶图,如下所示(满分
人对共享单车的评价得分统计填入茎叶图,如下所示(满分![]() 分):
分):

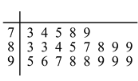
(1)找出居民问卷得分的众数和中位数;
(2)请计算这![]() 位居民问卷的平均得分;
位居民问卷的平均得分;
(3)若在成绩为![]() 分的居民中随机抽取
分的居民中随机抽取![]() 人,求恰有
人,求恰有![]() 人成绩超过
人成绩超过![]() 分的概率.
分的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com