
(1)求曲线C的方程;
(2)过点F(2,0)作斜率为k的直线l与曲线C交于A、B两点,若∠AOB为锐角,求实数k的取值范围.
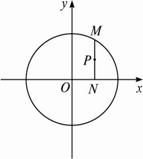
解:(1)设P(x,y),依题意点M(x,![]() y)在圆x2+y2=6上. ?
y)在圆x2+y2=6上. ?
∴x2+3y2=6,即曲线C的方程为![]() . ?
. ?
(2)方法一:因为直线l的斜率为k,所以可设方程为y=k(x-2),?
把直线l的方程代入曲线C方程得?
(1+3k2)x2-12k2x+12k2-6=0. ?
记A(x1,y1),B(x2,y2),则y1=k(x1-2),y2=k(x2-2).?
x1+x2=![]() ,x1x2=
,x1x2=![]() .?
.?
y1y2=k2[x1x2-2(x1+x2)+4]=k2(![]() -
-![]() +4)=
+4)=![]() . ?
. ?
∵∠AOB为锐角,∴![]() ·
·![]() =x1x2+y1y2=
=x1x2+y1y2=![]() >0.?
>0.?
解得k<-![]() ,或k>
,或k>![]() . ?
. ?
又Δ=144k4-4(1+3k2)(12k2-6)=24k2+24>0恒成立,![]() 与
与![]() 的方向不同.?
的方向不同.?
所以实数k的取值范围是k<-![]() ,或k>
,或k>![]() . ?
. ?
方法二:同方法一得到y1y2=![]() . ?
. ?
因为∠AOB为锐角,所以?
cos∠AOB=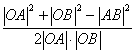 >0.?
>0.?
∵|OA|2=x12+y12,|OB|2=x22+y2,|AB|2=(x1-x2)2+(y1-y2)2,?
∴x12+y12+x22+y22-[(x1-x2)2+(y1-y2)2]=2(x1x2+y1y2)>0,即x1x2+y1y2=![]() >0.?
>0.?
解得k<-![]() ,或k>
,或k>![]() . ?
. ?
又Δ=144k4-4(1+3k2)(12k2-6)=24k2+24>0恒成立,
所以实数k的取值范围是k<-![]() ,或k>
,或k>![]() .
.


科目:高中数学 来源: 题型:
 圆锥曲线上任意两点连成的线段称为弦.若圆锥曲线上的一条弦垂直于其对称轴,我们将该弦称之为曲线的垂轴弦.已知点P(x0,y0)、M(m,n)是圆锥曲线C上不与顶点重合的任意两点,MN是垂直于x轴的一条垂轴弦,直线MP、NP分别交x轴于点E(xE,0)和点F(xF,0).
圆锥曲线上任意两点连成的线段称为弦.若圆锥曲线上的一条弦垂直于其对称轴,我们将该弦称之为曲线的垂轴弦.已知点P(x0,y0)、M(m,n)是圆锥曲线C上不与顶点重合的任意两点,MN是垂直于x轴的一条垂轴弦,直线MP、NP分别交x轴于点E(xE,0)和点F(xF,0).| x2 |
| a2 |
| y2 |
| b2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
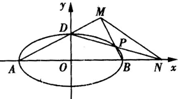 (2013•江西)椭圆C:
(2013•江西)椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 选做题:在A、B、C、D四小题中只能选做2题,每小题10分,共20分.解答应写出文字说明、证明过程或演算步骤.
选做题:在A、B、C、D四小题中只能选做2题,每小题10分,共20分.解答应写出文字说明、证明过程或演算步骤.
|
|
| 2 |
| π |
| 4 |
|
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2010•武昌区模拟)如图,已知椭圆
(2010•武昌区模拟)如图,已知椭圆| x2 |
| 4 |
| y2 |
| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com