
【题目】已知函数![]() (
(![]() 为自然对数的底数),
为自然对数的底数),![]()
![]() ,
,![]() .
.
(1)求曲线![]() 在
在![]() 处的切线方程;
处的切线方程;
(2)讨论函数![]() 的极小值;
的极小值;
(3)若对任意的![]() ,总存在
,总存在![]() ,使得
,使得![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
试题分析:(1)求出![]() 在
在![]() 处的导数即得切线的斜率;求出切点坐标,根据点斜式方程求得切线方程;(2)讨论导函数的零点
处的导数即得切线的斜率;求出切点坐标,根据点斜式方程求得切线方程;(2)讨论导函数的零点![]() 与定义域的关系得到其单调性,找出极小值点,求得极小值;(3)对任意的
与定义域的关系得到其单调性,找出极小值点,求得极小值;(3)对任意的![]() ,总存在
,总存在![]() ,使得
,使得![]() 成立,等价于
成立,等价于![]() 在
在![]() 上的最小值大于
上的最小值大于![]() 在
在![]() 上的最小值,分别求出
上的最小值,分别求出![]() 的最小值和
的最小值和![]() 的最小值,得到
的最小值,得到![]() 的范围.
的范围.
试题解析:(1)因为![]() ,
,
所以![]() ,即切线的斜率为
,即切线的斜率为![]() .
.
又![]() ,则切点坐标为
,则切点坐标为![]() ,
,
故曲线![]() 在
在![]() 处的切线方程为
处的切线方程为![]() ,
,
即![]() .
.
(2)![]()
![]() ,
,
![]() ,又
,又![]() 的定义域
的定义域![]() ,
,
∴当![]() 时,令
时,令![]() ,
,![]() 或
或![]() ,
,
令![]() ,
,![]() ,
,
∴![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,在
上单调递减,在![]() 单调递增,
单调递增,
∴![]() 的极小值为
的极小值为![]() ,
,
当![]() 时,
时,![]() ,
,
综上,![]() .
.
(3)对任意的![]() ,总存在
,总存在![]() ,
,
使得![]() 成立,等价于
成立,等价于![]() 在
在![]() 上的最小值大于
上的最小值大于![]() 在
在![]() 上的最小值,
上的最小值,
当![]() 时,
时,![]() ,
,
![]() 在
在![]() 上递减,
上递减,![]() ,
,
由(2)知,![]() 在
在![]() 上递增,
上递增,
![]() ,
,
∴![]() ,即
,即![]() ,又
,又![]() ,
,
∴![]() .
.


科目:高中数学 来源: 题型:
【题目】在四边形![]() 中,已知
中,已知![]() ,
,![]() ,点
,点![]() 在
在![]() 轴上,
轴上,![]() ,且对角线
,且对角线![]() .
.
(1)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)若点![]() 是直线
是直线![]() 上任意一点,过点
上任意一点,过点![]() 作点
作点![]() 的轨迹
的轨迹![]() 的两切线
的两切线![]() ,
,![]() 为切点,直线
为切点,直线![]() 是否恒过一定点?若是,请求出这个定点的坐标;若不是,请说明理由.
是否恒过一定点?若是,请求出这个定点的坐标;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
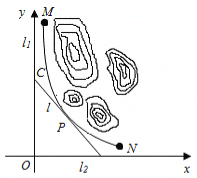
【题目】 某山区外围有两条相互垂直的直线型公路,为进一步改善山区的交通现状,计划修建一条连接两条公路的山区边界的直线型公路,记两条相互垂直的公路为![]() ,山区边界曲线为
,山区边界曲线为![]() ,计划修建的公路为
,计划修建的公路为![]() ,如图所示,
,如图所示,![]() 为
为![]() 的两个端点,测得点
的两个端点,测得点![]() 到
到![]() 的距离分别为5千米和40千米,点
的距离分别为5千米和40千米,点![]() 到
到![]() 的距离分别为20千米和2.5千米,以
的距离分别为20千米和2.5千米,以![]() 所在的直线分别为
所在的直线分别为![]() 轴,建立平面直角坐标系
轴,建立平面直角坐标系![]() ,假设曲线
,假设曲线![]() 符合函数
符合函数![]() (其中
(其中![]() 为常数)模型.
为常数)模型.
(1)求![]() 的值;
的值;
(2)设公路![]() 与曲线
与曲线![]() 相切于
相切于![]() 点,
点,![]() 的横坐标为
的横坐标为![]() .
.
①请写出公路![]() 长度的函数解析式
长度的函数解析式![]() ,并写出其定义域;
,并写出其定义域;
②当![]() 为何值时,公路
为何值时,公路![]() 的长度最短?求出最短长度.
的长度最短?求出最短长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校90名专职教师的年龄状况如下表:
年龄 | 35岁以下 | 35~50岁 | 50岁以上 |
人数 | 45 | 30 | 15 |
现拟采用分层抽样的方法从这90名专职教师中抽取6名老、中、青教师下乡支教一年.
(Ⅰ)求从表中三个年龄段中分别抽取的人数;
(Ⅱ)若从抽取的6个教师中再随机抽取2名到相对更加边远的乡村支教,计算这两名教师至少有一个年龄是35~50岁教师的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在长方体![]() 中,
中,![]() ,
,![]() 是棱
是棱![]() 上的一点.
上的一点.
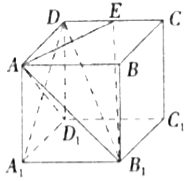
(1)求证:![]() 平面
平面![]() ;
;
(2)求证:![]() ;
;
(3)若![]() 是棱
是棱![]() 的中点,在棱
的中点,在棱![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求出线段
?若存在,求出线段![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若![]() ,且
,且![]() 在
在![]() 上单调递增,求实数
上单调递增,求实数![]() 的取值范围;
的取值范围;
(2)是否存在实数![]() ,使得函数
,使得函数![]() 在
在![]() 上的最小值为1?若存在,求出实数
上的最小值为1?若存在,求出实数![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,椭圆
,椭圆![]() 的离心率为
的离心率为![]() ,
, ![]() 是椭圆
是椭圆![]() 的右焦点,
的右焦点, ![]() 的斜率为
的斜率为![]() ,
, ![]() 为坐标原点.
为坐标原点.
(1)求椭圆![]() 的方程;
的方程;
(2)设过点![]() 的动直线
的动直线![]() 与
与![]() 交于
交于![]() ,
, ![]() 两点,当
两点,当![]() 面积最大时,求
面积最大时,求![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《中国好声音(![]()
![]()
![]()
![]() )》是由浙江卫视联合星空传媒旗下灿星制作强力打造的大型励志专业音乐评论节目,于2012年7月13日在浙江卫视播出.每期节目有四位导师参加.导师背对歌手,当每位参赛选手演唱完之前有导师为其转身,则该选手可以选择加入为其转身的导师的团队中接受指导训练.已知某期《中国好声音》中,6位选手唱完后,四位导师为其转身的情况如下表所示:
)》是由浙江卫视联合星空传媒旗下灿星制作强力打造的大型励志专业音乐评论节目,于2012年7月13日在浙江卫视播出.每期节目有四位导师参加.导师背对歌手,当每位参赛选手演唱完之前有导师为其转身,则该选手可以选择加入为其转身的导师的团队中接受指导训练.已知某期《中国好声音》中,6位选手唱完后,四位导师为其转身的情况如下表所示:
导师转身人数(人) | 4 | 3 | 2 | 1 |
获得相应导师转身的选手人数(人) | 1 | 2 | 2 | 1 |
现从这6位选手中随机抽取两人考查他们演唱完后导师的转身情况.
(1)请列出所有的基本事件;
(2)求两人中恰好其中一位为其转身的导师不少于3人,而另一人为其转身的导师不多于2人的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com