Question

【题目】某保险的基本保费为a（单位：元），继续购买该保险的投保人成为续保人，续保人本年度的保费与其上年度出险次数的关联如下：

上年度出险次数	0	1	2	3	4	≥5
保费	0.85a	a	1.25a	1.5a	1.75a	2a

设该险种一续保人一年内出险次数与相应概率如下：

一年内出险次数	0	1	2	3	4	≥5
概率	0.30	0.15	0.20	0.20	0.10	0.05

（Ⅰ）求一续保人本年度的保费高于基本保费的概率；
（Ⅱ）若一续保人本年度的保费高于基本保费，求其保费比基本保费高出60%的概率；
（Ⅲ）求续保人本年度的平均保费与基本保费的比值．

Answer 1

【答案】解：（Ⅰ）∵某保险的基本保费为a（单位：元），

上年度出险次数大于等于2时，续保人本年度的保费高于基本保费，

∴由该险种一续保人一年内出险次数与相应概率统计表得：

一续保人本年度的保费高于基本保费的概率：

p1=1﹣0.30﹣0.15=0.55．

（Ⅱ）设事件A表示“一续保人本年度的保费高于基本保费”，事件B表示“一续保人本年度的保费比基本保费高出60%”，

由题意P（A）=0.55，P（AB）=0.10+0.05=0.15，

由题意得若一续保人本年度的保费高于基本保费，

则其保费比基本保费高出60%的概率：

p2=P（B|A）= = = ．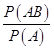

（Ⅲ）由题意，续保人本年度的平均保费与基本保费的比值为：

=1.23，

∴续保人本年度的平均保费与基本保费的比值为1.23

【解析】（Ⅰ）上年度出险次数大于等于2时，续保人本年度的保费高于基本保费，由此利用该险种一续保人一年内出险次数与相应概率统计表根据对立事件概率计算公式能求出一续保人本年度的保费高于基本保费的概率．（Ⅱ）设事件A表示“一续保人本年度的保费高于基本保费”，事件B表示“一续保人本年度的保费比基本保费高出60%”，由题意求出P（A），P（AB），由此利用条件概率能求出若一续保人本年度的保费高于基本保费，则其保费比基本保费高出60%的概率．（Ⅲ）由题意，能求出续保人本年度的平均保费与基本保费的比值．