
【题目】已知直线l的方程为![]() (
(![]() ).
).
(1)若直线l在两坐标轴上的截距相等,求直线l的方程;
(2)若直线l与x正半轴、射线![]() (
(![]() )分别交于P,Q两点,当a为何值时,
)分别交于P,Q两点,当a为何值时,![]() 的面积最小?
的面积最小?
科目:高中数学 来源: 题型:
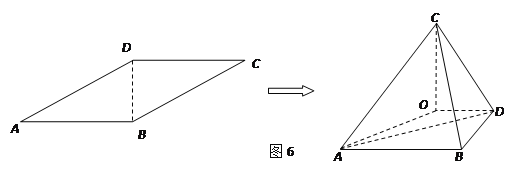
【题目】平行四边形![]() 中,
中,![]() ,沿
,沿![]() 将
将![]() 折起,使二面角
折起,使二面角![]() 是大小为锐角
是大小为锐角![]() 的二面角,设
的二面角,设![]() 在平面
在平面![]() 上的射影为
上的射影为![]() .
.
(1)当![]() 为何值时,三棱锥
为何值时,三棱锥![]() 的体积最大?最大值为多少?
的体积最大?最大值为多少?
(2)当![]() 时,求
时,求![]() 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某创业投资公司计划在2010年向某企业投入800万元用于开发新产品,并在今后若干年内,每年的投入资金都比上一年减少20%.估计2010年可获得投资回报收入400万元,由于该项投资前景广阔,预计今后的投资回报收入每年都会比上一年增加25%.
(Ⅰ)设第![]() 年(2010年为第一年)的投入资金为
年(2010年为第一年)的投入资金为![]() 万元,投资回报收入为
万元,投资回报收入为![]() 万元,求
万元,求![]() 和
和![]() 的表达式;
的表达式;
(Ⅱ)从哪一年开始,该投资公司前几年的投资回报总收入将超过总投入?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】假设要考察某公司生产的流感疫苗的剂量是否达标,现从500支疫苗中抽取50支进行检验,利用随机数表法抽取样本时,先将500支疫苗按![]() 进行编号,如果从随机数表第7行第8列的数开始向右读,请写出第3支疫苗的编号________.(下面摘取了随机数表第7行至第9行)
进行编号,如果从随机数表第7行第8列的数开始向右读,请写出第3支疫苗的编号________.(下面摘取了随机数表第7行至第9行)
第7行:84 42 17 53 31 57 24 55 06 88 77 04 74 47 67 21 76 33 50
25 83 92 12 06 76
第8行:63 01 63 78 59 16 95 56 67 19 98 10 50 71 75 12 86 73 58
07 44 39 52 38 79
第9行:33 21 12 34 29 78 64 56 07 82 52 42 07 44 38 15 51 00 13
42 99 66 02 79 54
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,且椭圆上一点与椭圆的两个焦点构成的三角形周长为
,且椭圆上一点与椭圆的两个焦点构成的三角形周长为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,且以
两点,且以![]() 为直径的圆过椭圆的右顶点
为直径的圆过椭圆的右顶点![]() ,求
,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥![]() 中,
中,![]() ,
,![]() 底面ABC.M,N分别为PB,PC的中点.
底面ABC.M,N分别为PB,PC的中点.
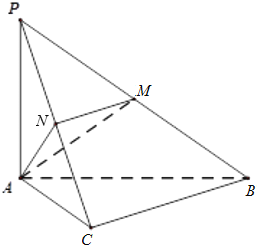
(1)求证:![]() 平面ABC;
平面ABC;
(2)求证:平面![]() 平面PAC;
平面PAC;
(3)若![]() ,求三棱锥
,求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正四棱锥S-ABCD中,O为顶点在底面内的投影,P为侧棱SD的中点,且SO=OD,则直线BC与平面PAC的夹角是

A. 30°B. 45°C. 60°D. 90°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com