
【题目】已知两点![]() 、
、![]() ,点
,点![]() 是直角坐标平面上的动点,若将点
是直角坐标平面上的动点,若将点![]() 的横坐标保持不变、纵坐标扩大到
的横坐标保持不变、纵坐标扩大到![]() 倍后得到点
倍后得到点![]() ,且满足
,且满足![]() .
.
(1)求动点![]() 所在曲线
所在曲线![]() 的方程;
的方程;
(2)过点![]() 作斜率为
作斜率为![]() 的直线
的直线![]() 交曲线
交曲线![]() 于
于![]() 、
、![]() 两点,且满足
两点,且满足![]() ,又点
,又点![]() 关于原点
关于原点![]() 的对称点为点
的对称点为点![]() ,求点
,求点![]() 、
、![]() 的坐标.
的坐标.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】下列说法正确的是______(将所有正确的序号都写出)
(1)直线![]() 及平面
及平面![]() ,若
,若![]() 且
且![]() ,则
,则![]() ;
;
(2)不同平面![]() ,若存在
,若存在![]() ,则
,则![]() ,其中
,其中![]() 是直线,且
是直线,且![]() ;
;
(3)已知![]() ,则
,则![]() ;
;
(4)平面![]() ,平面
,平面![]() ,则
,则![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
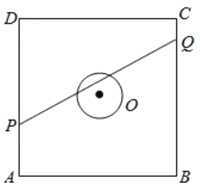
【题目】如图,正方形![]() 的边长为
的边长为![]() 米,圆
米,圆![]() 的半径为
的半径为![]() 米,圆心是正方形的中心,点
米,圆心是正方形的中心,点![]() 、
、![]() 分别在线段
分别在线段![]() 、
、![]() 上,若线段
上,若线段![]() 与圆
与圆![]() 有公共点,则称点
有公共点,则称点![]() 在点
在点![]() 的“盲区”中,已知点
的“盲区”中,已知点![]() 以
以![]() 米/秒的速度从
米/秒的速度从![]() 出发向
出发向![]() 移动,同时,点
移动,同时,点![]() 以
以![]() 米/秒的速度从
米/秒的速度从![]() 出发向
出发向![]() 移动,则在点
移动,则在点![]() 从
从![]() 移动到
移动到![]() 的过程中,点
的过程中,点![]() 在点
在点![]() 的盲区中的时长约________秒(精确到
的盲区中的时长约________秒(精确到![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,动圆
中,动圆![]() 与圆
与圆![]() 外切,且圆
外切,且圆![]() 与直线
与直线![]() 相切,记动圆圆心
相切,记动圆圆心![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的轨迹方程;
的轨迹方程;
(2)设过定点![]() 的动直线
的动直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,试问:在曲线
两点,试问:在曲线![]() 上是否存在点
上是否存在点![]() (与
(与![]() 两点相异),当直线
两点相异),当直线![]() 的斜率存在时,直线
的斜率存在时,直线![]() 的斜率之和为定值?若存在,求出点
的斜率之和为定值?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,且左焦点F1到左准线的距离为4.
,且左焦点F1到左准线的距离为4.

(1)求椭圆![]() 的方程;
的方程;
(2)若与原点距离为1的直线l1:![]() 与椭圆
与椭圆![]() 相交于A,B两点,直线l2与l1平行,且与椭圆
相交于A,B两点,直线l2与l1平行,且与椭圆![]() 相切于点M(O,M位于直线l1的两侧).记△MAB,△OAB的面积分别为S1,S2,若
相切于点M(O,M位于直线l1的两侧).记△MAB,△OAB的面积分别为S1,S2,若![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 的内角
的内角![]() 、
、![]() 、
、![]() 的对边分别为
的对边分别为![]() 、
、![]() 、
、![]() ,
,![]() 为
为![]() 内一点,若分别满足下列四个条件:
内一点,若分别满足下列四个条件:
①![]() ;
;
②![]() ;
;
③![]() ;
;
④![]() ;
;
则点![]() 分别为
分别为![]() 的( )
的( )
A.外心、内心、垂心、重心B.内心、外心、垂心、重心
C.垂心、内心、重心、外心D.内心、垂心、外心、重心
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着小汽车的普及,“驾驶证”已经成为现代人“必考”的证件之一.若某人报名参加了驾驶证考试,要顺利地拿到驾驶证,他需要通过四个科目的考试,其中科目二为场地考试.在一次报名中,每个学员有5次参加科目二考试的机会(这5次考试机会中任何一次通过考试,就算顺利通过,即进入下一科目考试;若5次都没有通过,则需重新报名),其中前2次参加科目二考试免费,若前2次都没有通过,则以后每次参加科目二考试都需要交200元的补考费.某驾校对以往2000个学员第1次参加科目二考试进行了统计,得到下表:
考试情况 | 男学员 | 女学员 |
第1次考科目二人数 | 1200 | 800 |
第1次通过科目二人数 | 960 | 600 |
第1次未通过科目二人数 | 240 | 200 |
若以上表得到的男、女学员第1次通过科目二考试的频率分别作为此驾校男、女学员每次通过科目二考试的概率,且每人每次是否通过科目二考试相互独立.现有一对夫妻同时在此驾校报名参加了驾驶证考试,在本次报名中,若这对夫妻参加科目二考试的原则为:通过科目二考试或者用完所有机会为止.
(1)求这对夫妻在本次报名中参加科目二考试都不需要交补考费的概率;
(2)若这对夫妻前2次参加科目二考试均没有通过,记这对夫妻在本次报名中参加科目二考试产生的补考费用之和为![]() 元,求
元,求![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com