
【题目】已知如图所示的三棱锥D﹣ABC的四个顶点均在球O的球面上,△ABC和△DBC所在平面相互垂直,AB=3,AC=![]() ,BC=CD=BD=2
,BC=CD=BD=2![]() ,则球O的表面积为( )
,则球O的表面积为( )
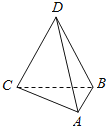
A.4π B.12π C.16π D.36π
科目:高中数学 来源: 题型:
【题目】为支援武汉的防疫,某医院职工踊跃报名,其中报名的医生18人,护士12人,医技6人,根据需要,从中抽取一个容量为n的样本参加救援队,若采用系统抽样和分层抽样,均不用剔除人员.当抽取n+1人时,若采用系统抽样,则需剔除1个报名人员,则抽取的救援人员为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两位战士参加射击比赛训练.从若干次预赛成绩中随机抽取8次,记录如下:
甲82 81 79 78 95 88 93 84
乙92 95 80 75 83 80 90 85
(1)用茎叶图表示这两组数据,并分别求两组数据的中位数;
(2)现要从中选派一人参加射击比赛,从统计学的角度考虑,你认为选派哪位战士参加合适?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2+ax+blnx(a,b∈R),曲线y=f(x)在点(1,f(1))处的切线方程为2x﹣y﹣2=0.
(1)判断f(x)在定义域内的单调性,并说明理由;
(2)若对任意的x∈(1,+∞),不等式f(x)≤m(ex﹣1﹣1)恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在锐角△ABC中,a=2![]() ,_______,求△ABC的周长l的范围.
,_______,求△ABC的周长l的范围.
在①![]() (﹣cos
(﹣cos![]() ,sin
,sin![]() ),
),![]() (cos
(cos![]() ,sin
,sin![]() ),且
),且![]()
![]() ,②cosA(2b﹣c)=acosC,③f(x)=cosxcos(x
,②cosA(2b﹣c)=acosC,③f(x)=cosxcos(x![]() )
)![]() ,f(A)
,f(A)![]()
注:这三个条件中任选一个,补充在上面问题中并对其进行求解.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,直线
中,直线![]() 过原点且倾斜角为
过原点且倾斜角为![]() .以坐标原点
.以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立坐标系,曲线
轴正半轴为极轴建立坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .在平面直角坐标系
.在平面直角坐标系![]() 中,曲线
中,曲线![]() 与曲线
与曲线![]() 关于直线
关于直线![]() 对称.
对称.
(Ⅰ)求曲线![]() 的极坐标方程;
的极坐标方程;
(Ⅱ)若直线![]() 过原点且倾斜角为
过原点且倾斜角为![]() ,设直线
,设直线![]() 与曲线
与曲线![]() 相交于
相交于![]() ,
,![]() 两点,直线
两点,直线![]() 与曲线
与曲线![]() 相交于
相交于![]() ,
,![]() 两点,当
两点,当![]() 变化时,求
变化时,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com