
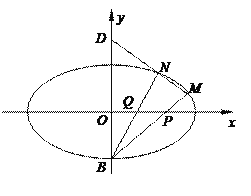
【题目】如图,在平面直角坐标系![]() 中,椭圆
中,椭圆![]() 的下顶点为
的下顶点为![]() ,点
,点![]() 是椭圆上异于点
是椭圆上异于点![]() 的动点,直线
的动点,直线![]() 分别与
分别与![]() 轴交于点
轴交于点![]() ,且点
,且点![]() 是线段
是线段![]() 的中点.当点
的中点.当点![]() 运动到点
运动到点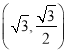 处时,点
处时,点![]() 的坐标为
的坐标为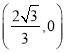 .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设直线![]() 交
交![]() 轴于点
轴于点![]() ,当点
,当点![]() 均在
均在![]() 轴右侧,且
轴右侧,且![]() 时,求直线
时,求直线![]() 的方程.
的方程.
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:(1)先求直线![]() 的方程,即得B坐标,有
的方程,即得B坐标,有![]() ;再将N坐标代入椭圆方程解得a(2)设直线
;再将N坐标代入椭圆方程解得a(2)设直线![]() 的斜率为
的斜率为![]() ,解得P点坐标,根据中点坐标公式得Q,利用直线方程与椭圆方程联立方程组解得M,N,根据横坐标之间比例关系求k,即得直线
,解得P点坐标,根据中点坐标公式得Q,利用直线方程与椭圆方程联立方程组解得M,N,根据横坐标之间比例关系求k,即得直线![]() 的方程.
的方程.
试题解析:解:(1)由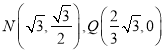 ,得直线
,得直线![]() 的方程为
的方程为![]() .
.
令![]() ,得点
,得点![]() 的坐标为
的坐标为![]() .
.
所以椭圆的方程为![]() .
.
将点![]() 的坐标
的坐标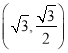 代入,得
代入,得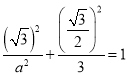 ,解得
,解得![]() .
.
所以椭圆![]() 的标准方程为
的标准方程为![]() .
.
(2)方法一:设直线![]() 的斜率为
的斜率为![]() ,则直线
,则直线![]() 的方程为
的方程为![]() .
.
在![]() 中,令
中,令![]() ,得
,得![]() ,而点
,而点![]() 是线段
是线段![]() 的中点,所以
的中点,所以![]() .
.
所以直线![]() 的斜率
的斜率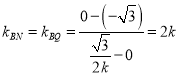 .
.
联立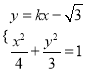 ,消去
,消去![]() ,得
,得![]() ,解得
,解得![]() .
.
用![]() 代
代![]() ,得
,得![]() .
.
又![]() ,所以
,所以![]() ,得
,得![]() .
.
故![]() ,又
,又![]() ,解得
,解得![]() .
.
所以直线![]() 的方程为
的方程为![]() .
.
方法二:设点![]() 的坐标分别为
的坐标分别为![]() .
.
由![]() ,得直线
,得直线![]() 的方程为
的方程为![]() ,令
,令![]() ,得
,得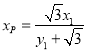 .
.
同理,得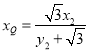 .
.
而点![]() 是线段
是线段![]() 的中点,所以
的中点,所以![]() ,故
,故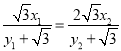 .
.
又![]() ,所以
,所以![]() ,得
,得![]() ,从而
,从而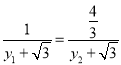 ,
,
解得![]() .
.
将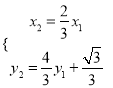 代入到椭圆C的方程中,得
代入到椭圆C的方程中,得 .
.
又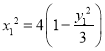 ,所以
,所以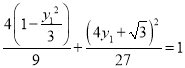 ,即
,即![]() ,
,
解得![]() (舍)或
(舍)或![]() .又
.又![]() ,所以点
,所以点![]() 的坐标为
的坐标为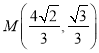 .
.
故直线![]() 的方程为
的方程为![]() .
.


 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的右焦点为
的右焦点为![]() ,上顶点为
,上顶点为![]() ,直线
,直线![]() 与直线
与直线![]() 垂直,椭圆
垂直,椭圆![]() 经过点
经过点![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)过点![]() 作椭圆
作椭圆![]() 的两条互相垂直的弦
的两条互相垂直的弦![]() .若弦
.若弦![]() 的中点分别为
的中点分别为![]() ,证明:直线
,证明:直线![]() 恒过定点.
恒过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (m,n∈R)在x=1处取得极值2.
(m,n∈R)在x=1处取得极值2.
(1)求f(x)的解析式;
(2)k为何值时,方程f(x)-k=0只有1个根
(3)设函数g(x)=x2-2ax+a,若对于任意x1∈R,总存在x2∈[-1,0],使得g(x2)≤f(x1),求a的取值范围
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图, ![]() 为圆柱
为圆柱![]() 的母线,
的母线, ![]() 是底面圆
是底面圆![]() 的直径,
的直径, ![]() 是
是![]() 的中点.
的中点.
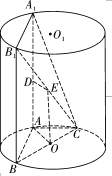
(Ⅰ)问: ![]() 上是否存在点
上是否存在点![]() 使得
使得![]() 平面
平面![]() ?请说明理由;
?请说明理由;
(Ⅱ)在(Ⅰ)的条件下,若![]() 平面
平面![]() ,假设这个圆柱是一个大容器,有条体积可以忽略不计的小鱼能在容器的任意地方游弋,如果小鱼游到四棱锥
,假设这个圆柱是一个大容器,有条体积可以忽略不计的小鱼能在容器的任意地方游弋,如果小鱼游到四棱锥![]() 外会有被捕的危险,求小鱼被捕的概率.
外会有被捕的危险,求小鱼被捕的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
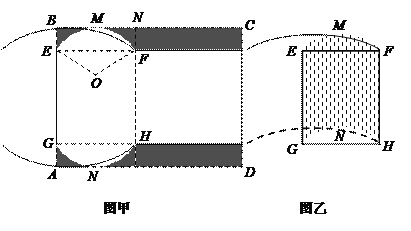
【题目】有一矩形硬纸板材料(厚度忽略不计),一边![]() 长为6分米,另一边足够长.现从中截取矩形
长为6分米,另一边足够长.现从中截取矩形![]() (如图甲所示),再剪去图中阴影部分,用剩下的部分恰好能折卷成一个底面是弓形的柱体包装盒(如图乙所示,重叠部分忽略不计),其中
(如图甲所示),再剪去图中阴影部分,用剩下的部分恰好能折卷成一个底面是弓形的柱体包装盒(如图乙所示,重叠部分忽略不计),其中![]() 是以
是以![]() 为圆心、
为圆心、![]() 的扇形,且弧
的扇形,且弧![]() ,
,![]() 分别与边
分别与边![]() ,
, ![]() 相切于点
相切于点![]() ,
, ![]() .
.
(1)当![]() 长为1分米时,求折卷成的包装盒的容积;
长为1分米时,求折卷成的包装盒的容积;
(2)当![]() 的长是多少分米时,折卷成的包装盒的容积最大?
的长是多少分米时,折卷成的包装盒的容积最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将圆![]() 上每个点的横坐标变为原来的4倍,纵坐标变为原来的3倍,得曲线
上每个点的横坐标变为原来的4倍,纵坐标变为原来的3倍,得曲线![]() ,以坐标原点为极点,
,以坐标原点为极点, ![]() 轴的非负轴分别交于
轴的非负轴分别交于![]() 半轴为极轴建立极坐标系,直线
半轴为极轴建立极坐标系,直线![]() 的极坐标方程为:
的极坐标方程为: ![]() ,且直线
,且直线![]() 在直角坐标系中与
在直角坐标系中与![]() 轴分别交于
轴分别交于![]() 两点.
两点.
(1)写出曲线![]() 的参数方程,直线
的参数方程,直线![]() 的普通方程;
的普通方程;
(2)问在曲线![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 的面积
的面积![]() ,若存在,求出点
,若存在,求出点![]() 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017年,世界乒乓球锦标赛在德国的杜赛尔多夫举行.整个比赛精彩纷呈,参赛选手展现出很高的竞技水平,为观众奉献了多场精彩对决.图1(扇形图)和表1是其中一场关键比赛的部分数据统计.两位选手在此次比赛中击球所使用的各项技术的比例统计如图1.在乒乓球比赛中,接发球技术是指回接对方发球时使用的各种方法.选手乙在比赛中的接发球技术统计如表1,其中的前4项技术统称反手技术,后3项技术统称为正手技术.

图1
选手乙的接发球技术统计表
技术 | 反手拧球 | 反手搓球 | 反手拉球 | 反手拨球 | 正手搓球 | 正手拉球 | 正手挑球 |
使用次数 | 20 | 2 | 2 | 4 | 12 | 4 | 1 |
得分率 | 55% | 50% | 0% | 75% | 41.7% | 75% | 100% |
表1
(Ⅰ)观察图1,在两位选手共同使用的8项技术中,差异最为显著的是哪两项技术?
(Ⅱ)乒乓球接发球技术中的拉球技术包括正手拉球和反手拉球.从表1统计的选手乙的所有拉球中任取两次,至少抽出一次反手拉球的概率是多少?
(Ⅲ)如果仅从表1中选手乙接发球得分率的稳定性来看(不考虑使用次数),你认为选手乙的反手技术更稳定还是正手技术更稳定?(结论不要求证明)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com