Question

已知f（x）=ax³+cx+d（a≠0）是R上的奇函数，当x=1时f（x）取得极值-2．
（Ⅰ）求f（x）的解析式；
（Ⅱ）求f（x）在（-4，5）上的单调区间．

Answer 1

解：（Ⅰ）由奇函数的定义，应有f（-x）=-f（x），x∈R
即-ax³-cx+d=-ax³-cx-d∴d=0
因此，f（x）=ax³+cx f'（x）=3ax²+c
由条件f（1）=-2为f（x）的极值，必有f'（1）=0，故
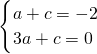
解得a=1，c=-3因此，f（x）=x³-3x，
（II）f'（x）=3x²-3=3（x+1）（x-1）
当x∈（-4，-1）时，f'（x）＞0，故f（x）在单调区间（-4，-1）上是增函数
当x∈（-1，1）时，f'（x）＜0，故f（x）在单调区间（-1，1）上是减函数
当x∈（1，5）时，f'（x）＞0，故f（x）在单调区间（1，5）上是增函数
分析：（I）根据奇函数的定义可求出d的值，然后根据f（1）=-2，f'（1）=0求出a与c的值，即可求出函数f（x）的解析式；
（II）先求导函数，然后在区间（-4，5）上解f'（x）＞0与f'（x）＜0的解集，即可求出函数的单调区间．
点评：本题主要考查了函数的奇偶性、函数在某点取得极值的条件和利用导数研究函数的单调性，同时考查了求单调区间的一般方法，属于中档题．