Question

已知函数f（x）=x²（ax+b），（a，b∈R）在x=2时有极值，其图象在点（1，f（1））处的切线与直线3x+y=0平行．
（1）求a、b的值和函数f（x）的单调区间；
（2）若当x∈[1，4]时，方程f（x）-t=0恰有一实根，试确定t的取值范围．

Answer 1

解：（1）因为函数f（x）=x²（ax+b）在x=2处取得极值，
所以 f'（2）=12a+4b=0①，
由图象在点（1，f（1））处的切线与直线3x+y=0平行，
则 f'（1）=3a+2b=-3②，
联立①②解得 a=1，b=-3，
代入f（x），得 f（x）=x³-3x²，此函数的定义域为（-∞，∞），
f'（x）=3x²-6x，
令f'（x）＞0，得x＜0或x＞2，令f′（x）＜0，得0＜x＜2，
所以函数f（x）在区间（-∞，0]和[2，∞）上是单调递增的；在区间（0，2）上是单调递减的；
（2）由（1）知：f（x）在[1，2]上单调递减，在[2，4]上单调递增，
当x=2时f（x）取得极小值，也即最小值为f（2）=8-12=-4，f（1）=1-3=-2，f（4）=64-48=16．
作出y=f（x）（1≤x≤4）的草图如下图所示：

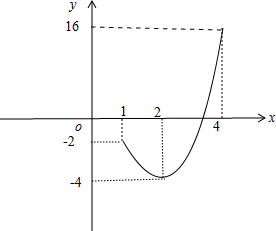
方程f（x）-t=0恰有一实根，即y=f（x）与y=t的图象只有一个交点，
由图象知：-2＜t≤16或t=-4．
故实数t的取值范围为：-2＜t≤16或t=-4．
分析：（1）由f（x）在x=2处有极值，得 f'（2）=0，由图象在点（1，f（1））处的切线与直线3x+y=0平行，得f'（1）=-3，联立方程组解出即可；
（2）借助（1）问结论作出f（x）在[1，4]上的草图，则方程f（x）-t=0恰有一实根即为y=f（x）与y=t的图象只有一个交点，由图象即可求得范围．
点评：本题考查利用导数研究函数的极值、单调性及方程根的个数问题，考查数形结合思想，考查学生分析解决问题的能力，属中档题．