
【题目】网购逐步走入百姓生活,网络(电子)支付方面的股票受到一些股民的青睐.某单位4位热爱炒股的好朋友研究后决定购买“生意宝”和“九州通“这两支股票中的一支.他们约定:每人通过掷一枚质地均匀的骰子决定购买哪支股票,掷出点数为5或6的人买“九州通”股票,掷出点数为小于5的人买“生意宝”股票,且必须从“生意宝”和“九州通”这两支股票中选择一支股票购买.
(1)求这4人中恰有1人购买“九州通”股票的機率;
(2)用![]() ,
,![]() 分别表示这4人中购买“生意宝”和“九州通”股票的人数,记
分别表示这4人中购买“生意宝”和“九州通”股票的人数,记![]() ,求随机变量X的分布列与数学期望
,求随机变量X的分布列与数学期望![]() .
.
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,AD∥BC,![]() ADC=
ADC=![]() PAB=90°,BC=CD=
PAB=90°,BC=CD=![]() AD.E为棱AD的中点,异面直线PA与CD所成的角为90°.
AD.E为棱AD的中点,异面直线PA与CD所成的角为90°.

(I)在平面PAB内找一点M,使得直线CM∥平面PBE,并说明理由;
(II)若二面角P-CD-A的大小为45°,求直线PA与平面PCE所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,短轴长为
,短轴长为![]() .
.
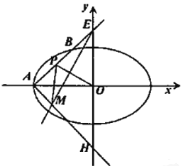
(1)求![]() 的方程;
的方程;
(2)如图,经过椭圆左顶点![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 与
与![]() 交于
交于![]() 两点,交
两点,交![]() 轴于点
轴于点![]() ,点
,点![]() 为线段
为线段![]() 的中点,若点
的中点,若点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,过点
,过点![]() 作
作![]() (
(![]() 为坐标原点)垂直的直线交直线
为坐标原点)垂直的直线交直线![]() 于点
于点![]() ,且
,且![]() 面积为
面积为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直角梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,直角梯形
,直角梯形![]() 可以通过直角梯形
可以通过直角梯形![]() 以直线
以直线![]() 为轴旋转得到,且平面
为轴旋转得到,且平面![]() 平面
平面![]() .
.
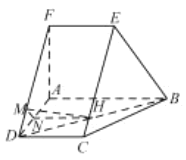
(1)求证:![]() ;
;
(2)设![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点,
的中点,![]() 为线段
为线段![]() 上的点(不与点
上的点(不与点![]() 重合).
重合).
(i)若平面![]() 平面
平面![]() ,求
,求![]() 的长;
的长;
(ii)线段![]() 上是否存在
上是否存在![]() ,使得直线
,使得直线![]() 平面
平面![]() ,若存在求
,若存在求![]() 的长,若不存在说明理由.
的长,若不存在说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形![]() 与
与![]() 均为菱形,
均为菱形,![]() ,且
,且![]() .
.
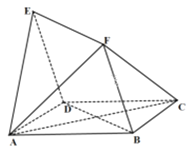
(1)求证:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值;
的余弦值;
(3)若![]() 为线段
为线段![]() 上的一点,满足直线
上的一点,满足直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中函数
,其中函数![]() ,
,![]() .
.
(1)求函数![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)当![]() 时,求函数
时,求函数![]() 在
在![]() 上的最大值;
上的最大值;
(3)当![]() 时,对于给定的正整数
时,对于给定的正整数![]() ,问:函数
,问:函数![]() 是否有零点?请说明理由.(参考数据
是否有零点?请说明理由.(参考数据![]() ,
,![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若无穷数列![]() 满足:
满足:![]() 是正实数,当
是正实数,当![]() 时,
时,![]() ,则称
,则称![]() 是“
是“![]() —数列”.
—数列”.
(1)若![]() 是“
是“![]() —数列”且
—数列”且![]() ,写出
,写出![]() 的所有可能值;
的所有可能值;
(2)设![]() 是“
是“![]() —数列”,证明:
—数列”,证明:![]() 是等差数列当且仅当
是等差数列当且仅当![]() 单调递减;
单调递减;![]() 是等比数列当且仅当
是等比数列当且仅当![]() 单调递增;
单调递增;
(3)若![]() 是“
是“![]() —数列”且是周期数列(即存在正整数
—数列”且是周期数列(即存在正整数![]() ,使得对任意正整数
,使得对任意正整数![]() ,都有
,都有![]() ),求集合
),求集合![]() 的元素个数的所有可能值的个数.
的元素个数的所有可能值的个数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com