
【题目】某大学为调研学生在A,B两家餐厅用餐的满意度,从在A,B两家餐厅都用过餐的学生中随机抽取了100人,每人分别对这两家餐厅进行评分,满分均为60分.整理评分数据,将分数以10为组距分成6组:[0,10),[10,20),[20,30),[30,40),[40,50),[50,60],得到A餐厅分数的频率分布直方图,和B餐厅分数的频数分布表:
B餐厅分数频数分布表 | |
分数区间 | 频数 |
[0,10) | 2 |
[10,20) | 3 |
[20,30) | 5 |
[30,40) | 15 |
[40,50) | 40 |
[50,60] | 35 |
定义学生对餐厅评价的“满意度指数”如下:
分数 | [0,30) | [30,50) | [50,60] |
满意度指数 | 0 | 1 | 2 |

(Ⅰ)在抽样的100人中,求对A餐厅评价“满意度指数”为0的人数;
(Ⅱ)从该校在A,B两家餐厅都用过餐的学生中随机抽取1人进行调查,试估计其对A餐厅评价的“满意度指数”比对B餐厅评价的“满意度指数”高的概率;
(Ⅲ)如果从A,B两家餐厅中选择一家用餐,你会选择哪一家?说明理由.
【答案】解:(Ⅰ)由对A餐厅评分的频率分布直方图,得
对A餐厅“满意度指数”为0的频率为(0.003+0.005+0.012)×10=0.2,
所以,对A餐厅评价“满意度指数”为0的人数为100×0.2=20.
(Ⅱ)设“对A餐厅评价‘满意度指数’比对B餐厅评价‘满意度指数’高”为事件C.
记“对A餐厅评价‘满意度指数’为1”为事件A1;“对A餐厅评价‘满意度指数’为2”为事件A2;“对B餐厅评价‘满意度指数’为0”为事件B0;“对B餐厅评价‘满意度指数’为1”为事件B1.
所以P(A1)=(0.02+0.02)×10=0.4,P(A2)=0.4,
由用频率估计概率得: ![]() ,
, ![]() .
.
因为事件Ai与Bj相互独立,其中i=1,2,j=0,1.
所以P(C)=P(A1B0+A2B0+A2B1)
=0.4×0.1+0.4×0.1+0.4×0.55=0.3.
所以该学生对A餐厅评价的“满意度指数”比对B餐厅评价的“满意度指数”高
的概率为0.3.
(Ⅲ)如果从学生对A,B两家餐厅评价的“满意度指数”的期望角度看:
A餐厅“满意度指数”X的分布列为:
X | 0 | 1 | 2 |
P | 0.2 | 0.4 | 0.4 |
B餐厅“满意度指数”Y的分布列为:
Y | 0 | 1 | 2 |
P | 0.1 | 0.55 | 0.35 |
因为EX=0×0.2+1×0.4+2×0.4=1.2;
EY=0×0.1+1×0.55+2×0.35=1.25,
所以EX<EY,会选择B餐厅用餐
【解析】(Ⅰ)由对A餐厅评分的频率分布直方图,求解对A餐厅“满意度指数”为0的频率.然后求解对A餐厅评价“满意度指数”为0的人数.(Ⅱ)设“对A餐厅评价‘满意度指数’比对B餐厅评价‘满意度指数’高”为事件C.记“对A餐厅评价‘满意度指数’为1”为事件A1;“对A餐厅评价‘满意度指数’为2”为事件A2;“对B餐厅评价‘满意度指数’为0”为事件B0;“对B餐厅评价‘满意度指数’为1”为事件B1.求出概率,利用独立重复概率乘法公式求解即可.(Ⅲ)从学生对A,B两家餐厅评价的“满意度指数”的期望角度看:得到分布列,求出期望,即可推出结果.
【考点精析】解答此题的关键在于理解离散型随机变量及其分布列的相关知识,掌握在射击、产品检验等例子中,对于随机变量X可能取的值,我们可以按一定次序一一列出,这样的随机变量叫做离散型随机变量.离散型随机变量的分布列:一般的,设离散型随机变量X可能取的值为x1,x2,.....,xi,......,xn,X取每一个值 xi(i=1,2,......)的概率P(ξ=xi)=Pi,则称表为离散型随机变量X 的概率分布,简称分布列.


 小学教材完全解读系列答案
小学教材完全解读系列答案科目:高中数学 来源: 题型:
【题目】《中国诗词大会》(第二季)亮点颇多,十场比赛每场都有一首特别设计的开场诗词,在声光舞美的配合下,百人团齐声朗诵,别有韵味.若《将进酒》《山居秋暝》《望岳》《送杜少府之任蜀州》和另确定的两首诗词排在后六场,且《将进酒》排在《望岳》的前面,《山居秋暝》与《送杜少府之任蜀州》不相邻且均不排在最后,则后六场的排法有( )
A.144种
B.288种
C.360种
D.720种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线l的参数方程为 ![]() (t为参数),其中0≤α<π.在以O为极点,x轴的正半轴为极轴的极坐标系中,曲线C1:ρ=4cosθ.直线l与曲线C1相切.
(t为参数),其中0≤α<π.在以O为极点,x轴的正半轴为极轴的极坐标系中,曲线C1:ρ=4cosθ.直线l与曲线C1相切.
(1)将曲线C1的极坐标方程化为直角坐标方程,并求α的值.
(2)已知点Q(2,0),直线l与曲线C2:x2+ ![]() =1交于A,B两点,求△ABQ的面积.
=1交于A,B两点,求△ABQ的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】据统计,某物流公司每天的业务中,从甲地到乙地的可配送的货物量X(40≤X<200,单位:件)的频率分布直方图,如图所示,将频率视为概率,回答以下问题. 
(1)求该物流公司每天从甲地到乙地平均可配送的货物量;
(2)该物流公司拟购置货车专门运营从甲地到乙地的货物,一辆货车每天只能运营一趟,每辆车每 趟最多只能装载40 件货物,满载发车,否则不发车.若发车,则每辆车每趟可获利1000 元;若未发车,
则每辆车每天平均亏损200 元.为使该物流公司此项业务的营业利润最大,该物流公司应该购置几辆货
车?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在几何体ABCDEF中,底面ABCD为矩形,EF∥CD,CD⊥EA,CD=2EF=2,ED= ![]() .M为棱FC上一点,平面ADM与棱FB交于点N.
.M为棱FC上一点,平面ADM与棱FB交于点N. 
(Ⅰ)求证:ED⊥CD;
(Ⅱ)求证:AD∥MN;
(Ⅲ)若AD⊥ED,试问平面BCF是否可能与平面ADMN垂直?若能,求出 ![]() 的值;若不能,说明理由.
的值;若不能,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在棱长为1的正方体ABCD﹣A1B1C1D1中,点P是线段BD1上的动点.当△PAC在平面DC1 , BC1 , AC上的正投影都为三角形时,将它们的面积分别记为S1 , S2 , S3 . 
(i)当BP= ![]() 时,S1S2(填“>”或“=”或“<”);
时,S1S2(填“>”或“=”或“<”);
(ii) S1+S2+S3的最大值为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC的三个内角A、B、C所对的边长分别是a、b、c,且 ![]() ,若将函数f(x)=2sin(2x+B)的图象向右平移
,若将函数f(x)=2sin(2x+B)的图象向右平移 ![]() 个单位长度,得到函数g(x)的图象,则g(x)的解析式为( )
个单位长度,得到函数g(x)的图象,则g(x)的解析式为( )
A.![]()
B.![]()
C.2sin2x
D.2cos2x
查看答案和解析>>
科目:高中数学 来源: 题型:
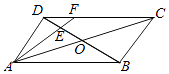
【题目】在平行四边形ABCD中,AC与BD交于点O,E是线段OD的中点,AE的延长线与CD相交于点F.若AB=2, ![]() ,∠BAD=45°,则
,∠BAD=45°,则 ![]() =( )
=( )
A.![]()
B.1
C.﹣ ![]()
D.1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为研究学生语言学科的学习情况,现对高二200名学生英语和语文某次考试成绩进行抽样分析.将200名学生编号为001,002,…,200,采用系统抽样的方法等距抽取10名学生,将10名学生的两科成绩(单位:分)绘成折线图如下: 
(Ⅰ)若第一段抽取的学生编号是006,写出第五段抽取的学生编号;
(Ⅱ)在这两科成绩差超过20分的学生中随机抽取2人进行访谈,求2人成绩均是语文成绩高于英语成绩的概率;
(Ⅲ)根据折线图,比较该校高二年级学生的语文和英语两科成绩,写出你的结论和理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com