
【题目】2020年初,由于疫情影响,开学延迟,为了不影响学生的学习,国务院、省市区教育行政部门倡导各校开展“停学不停课、停学不停教”,某校语文学科安排学生学习内容包含老师推送文本资料学习和视频资料学习两类,且这两类学习互不影响已知其积分规则如下:每阅读一篇文本资料积1分,每日上限积5分;观看视频1个积2分,每日上限积6分.经过抽样统计发现,文本资料学习积分的概率分布表如表1所示,视频资料学习积分的概率分布表如表2所示.
表1
文本学习积分 | 1 | 2 | 3 | 4 | 5 |
概率 |
|
|
|
|
|
表2
视频学习积分 | 2 | 4 | 6 |
概率 |
|
|
|
(1)现随机抽取1人了解学习情况,求其每日学习积分不低于9分的概率;
(2)现随机抽取3人了解学习情况,设积分不低于9分的人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
【答案】(1)![]() ;(2)分布列详见解析,数学期望为
;(2)分布列详见解析,数学期望为![]() .
.
【解析】
(1)由题意可得获得的积分不低于(9分)的情形,因为两类学习互不影响,根据相互独立与互斥事件的概率计算公式即可得出概率![]() .
.
(2)随机变量![]() 的所有可能取值为0,1,2,3.由(1)每个人积分不低于(9分)的概率为
的所有可能取值为0,1,2,3.由(1)每个人积分不低于(9分)的概率为![]() .根据二项分布列的概率计算公式即可得出.
.根据二项分布列的概率计算公式即可得出.
(1)由题意,获得的积分不低于9分的情形共有(如下表所示):
文本 | 3 | 4 | 5 | 5 |
视频 | 6 | 6 | 6 | 4 |
因为两类学习情况互不影响,
所以每日学习积分不低于9分的概率![]() ,
,
即每日学习积分不低于9分的概率为![]() .
.
(2)随机变量![]() 的所有可能取值为0,1,2,3
的所有可能取值为0,1,2,3
由(1)每个人积分不低于9分的概率为![]() .
.
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
所以随机变量![]() 的概率分布列为:
的概率分布列为:
| 0 | 1 | 2 | 3 |
P |
|
|
|
|
可得![]() .
.
所以随机变量![]() 的数学期望为
的数学期望为![]() .
.


科目:高中数学 来源: 题型:
【题目】某厂家准备在“6.18”举行促销活动,现根据近七年的广告费与销售量的数据确定此次广告费支出.广告费支出x(万元)和销售量y(万台)的数据如下:
年份 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 |
广告费支出x | 1 | 2 | 4 | 6 | 11 | 13 | 19 |
销售量y | 1.8 | 3.0 | 4.0 | 4.2 | 5.0 | 5.3 | 5.4 |
(1)若用线性回归模型拟合y与x的关系,求出y关于x的线性回归方程(保留小数点后两位);
(2)若用![]() 模型拟合y与x的关系,可得回归方程
模型拟合y与x的关系,可得回归方程![]() ,经计算线性回归模型和该模型的R2分别约为0.774和0.888,请用R2说明选择哪个回归模型更好;
,经计算线性回归模型和该模型的R2分别约为0.774和0.888,请用R2说明选择哪个回归模型更好;
(3)已知利润z与x,y的关系为z=200y-x.根据(2)的结果,当广告费x=20时,求销售量及利润的预报值.
参考公式:回归直线![]() =
=![]() +
+![]() x的斜率和截距的最小二乘估计分别为
x的斜率和截距的最小二乘估计分别为![]() =
=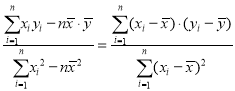 ,
,![]() .
.
参考数据:![]() ≈2.24,
≈2.24,![]() ,
, ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】目前,新冠病毒引发的肺炎疫情在全球肆虐,为了解新冠肺炎传播途径,采取有效防控措施,某医院组织专家统计了该地区![]() 名患者新冠病毒潜伏期的相关信息,数据经过汇总整理得到如下图所示的频率分布直方图(用频率作为概率).潜伏期不高于平均数的患者,称为“短潜伏者”,潜伏期高于平均数的患者,称为“长潜伏者”.
名患者新冠病毒潜伏期的相关信息,数据经过汇总整理得到如下图所示的频率分布直方图(用频率作为概率).潜伏期不高于平均数的患者,称为“短潜伏者”,潜伏期高于平均数的患者,称为“长潜伏者”.
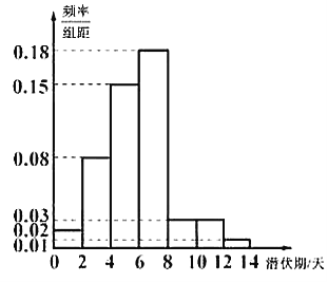
(1)求这![]() 名患者潜伏期的平均数(同一组中的数据用该组区间的中点值作代表),并计算出这
名患者潜伏期的平均数(同一组中的数据用该组区间的中点值作代表),并计算出这![]() 名患者中“长潜伏者”的人数;
名患者中“长潜伏者”的人数;
(2)现有![]() 名患者自愿报名某临床试验,其中“短潜伏者”
名患者自愿报名某临床试验,其中“短潜伏者”![]() 人,“长潜伏者”
人,“长潜伏者”![]() 人,医生从
人,医生从![]() 人中随机抽取两人做临床试验,求两人中恰有
人中随机抽取两人做临床试验,求两人中恰有![]() 人为“长潜伏者”的概率.
人为“长潜伏者”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在对人们休闲方式的一次调查中,共调查120人,其中女性70人,男性50人.女性中有40人主要的休闲方式是看电视,另外30人主要的休闲方式是运动;男性中有20人主要的休闲方式是看电视,另外30人主要的休闲方式是运动.
(1)请画出性别与休闲方式的![]() 列联表;
列联表;
(2)能否在犯错误的概率不超过0.10的前提下,认为休闲方式与性别有关?
附: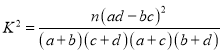 ,
,
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《山东省高考改革试点方案》规定:从2017年秋季高中入学的新生开始,不分文理科;2020年高考总成绩由语数外三门统考科目和物理、化学等六门选考科目组成,将每门选考科目的考生原始成绩从高到低划分为![]() 、
、![]() 、
、![]() 、
、![]() 共8个等级,参照正态分布原则,确定各等级人数所占比例分别为3%、7%、16%、24%、24%、16%、7%、3%,选考科目成绩计入考生总成绩时,将A至E等级内的考生原始成绩,依照等比例转换法则,分别转换到
共8个等级,参照正态分布原则,确定各等级人数所占比例分别为3%、7%、16%、24%、24%、16%、7%、3%,选考科目成绩计入考生总成绩时,将A至E等级内的考生原始成绩,依照等比例转换法则,分别转换到![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,
,![]() 八个分数区间,得到考生的等级成绩.某市高一学生共6000人,为给高一学生合理选科提供依据,对六门选考科目进行测试,其中化学考试原始成绩
八个分数区间,得到考生的等级成绩.某市高一学生共6000人,为给高一学生合理选科提供依据,对六门选考科目进行测试,其中化学考试原始成绩![]() 大致服从正态分布
大致服从正态分布![]() .
.
(1)求该市化学原始成绩在区间![]() 的人数;
的人数;
(2)以各等级人数所占比例作为各分数区间发生的概率,按高考改革方案,若从全省考生中随机抽取3人,记X表示这3人中等级成绩在区间![]() 的人数,求
的人数,求![]() .
.
(附:若随机变量![]() ,则
,则![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数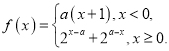 给出下列四个结论:①对
给出下列四个结论:①对![]() ,
,![]() ,使得
,使得![]() 无解;②对
无解;②对![]() ,
,![]() ,使得
,使得![]() 有两解;③当
有两解;③当![]() 时,
时,![]() ,使得
,使得![]() 有解;④当
有解;④当![]() 时,
时,![]() ,使得
,使得![]() 有三解.其中,所有正确结论的序号是______.
有三解.其中,所有正确结论的序号是______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() .已知点
.已知点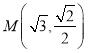 在椭圆上,且点M到两焦点距离之和为4.
在椭圆上,且点M到两焦点距离之和为4.
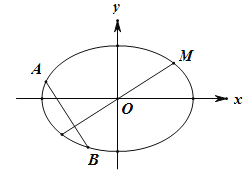
(1)求椭圆的方程;
(2)设与MO(O为坐标原点)垂直的直线交椭圆于A,B(A,B不重合),求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列有关说法正确的是( )
A.![]() 的展开式中含
的展开式中含![]() 项的二项式系数为20;
项的二项式系数为20;
B.事件![]() 为必然事件,则事件
为必然事件,则事件![]() 、
、![]() 是互为对立事件;
是互为对立事件;
C.设随机变量![]() 服从正态分布
服从正态分布![]() ,若
,若![]() ,则
,则![]() 与
与![]() 的值分别为
的值分别为![]() ,
,![]() ;
;
D.甲、乙、丙、丁4个人到4个景点旅游,每人只去一个景点,设事件![]() “4个人去的景点各不相同”,事件
“4个人去的景点各不相同”,事件![]() “甲独自去一个景点”,则
“甲独自去一个景点”,则![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com