
【题目】给出下列命题: ①把函数y=sin(x﹣ ![]() )图象上所有点的横坐标缩短到原来的
)图象上所有点的横坐标缩短到原来的 ![]() 倍,纵坐标不变,得到函数y=sin(2x﹣
倍,纵坐标不变,得到函数y=sin(2x﹣ ![]() );
);
②若α,β是第一象限角且α<β,则cosα>cosβ;
③x=﹣ ![]() 是函数y=cos(2x+
是函数y=cos(2x+ ![]() π)的一条对称轴;
π)的一条对称轴;
④函数y=4sin(2x+ ![]() )与函数y=4cos(2x﹣
)与函数y=4cos(2x﹣ ![]() )相同;
)相同;
⑤y=2sin(2x﹣ ![]() )在[0,
)在[0, ![]() ]是增函数;
]是增函数;
则正确命题的序号 .
【答案】①③④
【解析】解:对于①,把函数y=sin(x﹣ ![]() )图象上所有点的横坐标缩短到原来的
)图象上所有点的横坐标缩短到原来的 ![]() 倍,纵坐标不变,得到函数y=sin(2x﹣
倍,纵坐标不变,得到函数y=sin(2x﹣ ![]() ),故①正确. 对于②,当α,β是第一象限角且α<β,如α=30°,β=390°,则此时有cosα=cosβ=
),故①正确. 对于②,当α,β是第一象限角且α<β,如α=30°,β=390°,则此时有cosα=cosβ= ![]() ,故②错误.
,故②错误.
对于③,当x=﹣ ![]() 时,2x+
时,2x+ ![]() π=π,函数y=cos(2x+
π=π,函数y=cos(2x+ ![]() π)=﹣1,为函数的最小值,故x=﹣
π)=﹣1,为函数的最小值,故x=﹣ ![]() 是函数y=cos(2x+
是函数y=cos(2x+ ![]() π)的一条对称轴,故③正确.
π)的一条对称轴,故③正确.
对于④,函数y=4sin(2x+ ![]() )=4cos[
)=4cos[ ![]() ﹣(2x+
﹣(2x+ ![]() )]=4cos(
)]=4cos( ![]() ﹣2)=4cos(2x﹣
﹣2)=4cos(2x﹣ ![]() ),
),
故函数y=4sin(2x+ ![]() )与函数y=4cos(2x﹣
)与函数y=4cos(2x﹣ ![]() )相同,故④正确.
)相同,故④正确.
对于⑤,在[0, ![]() ]上,2x﹣
]上,2x﹣ ![]() ∈[﹣
∈[﹣ ![]() ,
, ![]() ],函数y=2sin(2x﹣
],函数y=2sin(2x﹣ ![]() )在[0,
)在[0, ![]() ]上没有单调性,故⑤错误,
]上没有单调性,故⑤错误,
所以答案是:①③④.
【考点精析】认真审题,首先需要了解函数y=Asin(ωx+φ)的图象变换(图象上所有点向左(右)平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的横坐标伸长(缩短)到原来的
的图象上所有点的横坐标伸长(缩短)到原来的![]() 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的纵坐标伸长(缩短)到原来的
的图象上所有点的纵坐标伸长(缩短)到原来的![]() 倍(横坐标不变),得到函数
倍(横坐标不变),得到函数![]() 的图象).
的图象).


 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:高中数学 来源: 题型:
【题目】如图(1),五边形![]() 中,
中, ![]() .如图(2),将
.如图(2),将![]() 沿
沿![]() 折到
折到![]() 的位置,得到四棱锥
的位置,得到四棱锥![]() .点
.点![]() 为线段
为线段![]() 的中点,且
的中点,且![]() 平面
平面![]() .
.
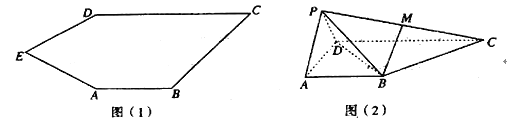
(1)求证:平面![]() 平面
平面![]() ;
;
(2)若直线![]() 与
与![]() 所成角的正切值为
所成角的正切值为![]() ,设
,设![]() ,求四棱锥
,求四棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)是定义在R上的偶函数,对任意x∈R,都有f(x+4π)=f(x)+f(2π)成立,那么函数f(x)可能是( )
A.f(x)=2sin ![]() x
x
B.f(x)=2cos2 ![]() x
x
C.f(x)=2cos2 ![]() x
x
D.f(x)=2cos ![]() x
x
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是七位评委为甲,乙两名参赛歌手打出的分数的茎叶图(其中m,n为数字0~9中的一个),则甲歌手得分的众数和乙歌手得分的中位数分别为a和b,则一定有( ) 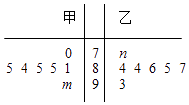
A.a>b
B.a<b
C.a=b
D.a,b的大小与m,n的值有关
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是根据部分城市某年6月份的平均气温(单位:℃)数据得到的样本频率分布直方图,其中平均气温的范围是[20.5,26.5].已知样本中平均气温不大于22.5℃的城市个数为11,则样本中平均气温不低于25.5℃的城市个数为 . 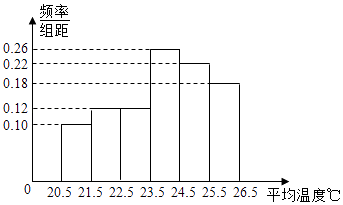
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=cos(ωx+ ![]() ),(ω>0,0<φ<π),其中x∈R且图象相邻两对称轴之间的距离为
),(ω>0,0<φ<π),其中x∈R且图象相邻两对称轴之间的距离为 ![]() ;
;
(1)求f(x)的对称轴方程和单调递增区间;
(2)求f(x)的最大值、最小值,并指出f(x)取得最大值、最小值时所对应的x的集合.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C所对的边分别为a,b,c,设S为△ABC的面积,满足S= ![]() (a2+b2﹣c2).
(a2+b2﹣c2).
(1)求角C的大小;
(2)求sinA+sinB的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(12分)已知椭圆C:![]() (a>b>0),四点P1(1,1),P2(0,1),P3(–1,
(a>b>0),四点P1(1,1),P2(0,1),P3(–1,![]() ),P4(1,
),P4(1,![]() )中恰有三点在椭圆C上.
)中恰有三点在椭圆C上.
(1)求C的方程;
(2)设直线l不经过P2点且与C相交于A,B两点.若直线P2A与直线P2B的斜率的和为–1,证明:l过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知过点P(m,n)的直线l与直线l0:x+2y+4=0垂直. (Ⅰ)若 ![]() ,且点P在函数
,且点P在函数 ![]() 的图像上,求直线l的一般式方程;
的图像上,求直线l的一般式方程;
(Ⅱ)若点P(m,n)在直线l0上,判断直线mx+(n﹣1)y+n+5=0是否经过定点?若是,求出该定点的坐标;否则,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com