
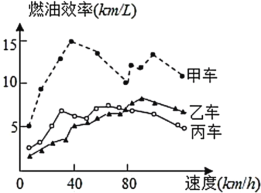
����Ŀ�������ġ�ȼ��Ч�ʡ���ָ����ÿ����1��������ʻ����̣���ͼ�����˼ס��ҡ������������ڲ�ͬ�ٶ��µ�ȼ��Ч������������������������ǣ� ��
A.����1�������ҳ�������ʻ5ǧ��.
B.����ͬ�ٶ���ʻ��ͬ·�̣��������У��׳������������.
C.�׳���80ǧ��/Сʱ���ٶ���ʻ1Сʱ������10������.
D.ij���л������������80ǧ��/Сʱ����ͬ�����£��ڸ����ñ��������ҳ���ʡ��.
���𰸡�ABC
��������
��������ijһ���������ƽ���ߣ������ߺ��������ߵĽ������˼����ͬ�ٶ��µ��������IJ�ͬ��ȼ��Ч�ʣ���������ijһ���������ƽ���ߣ������ߺ��������ߵĽ������˼����ͬȼ��Ч���µ��������IJ�ͬ���ٶȣ�������һ��Ϳ��Ժܿ������⣮�漰����ͼ������ת��Ϊ��ѧ���Ե������ͼ�����������.
�⣺����A����ͼ���֪���ٶȴ���40km/hʱ���ҳ���ȼ��Ч�ʴ���5km/L��
�൱�ٶȴ���40km/hʱ������1�����ͣ��ҳ�����ʻ�������5km����A����
����B����ͼ���֪���ٶ���ͬʱ���׳���ȼ��Ч����ߣ������ٶ���ͬʱ������1�����ͣ��׳�����ʻ·����Զ��
������ͬ�ٶ���ʻ��ͬ·�̣��������У��׳������������٣���B����
����C����ͼ���֪���ٶ�Ϊ80km/hʱ���׳���ȼ��Ч��Ϊ10km/L�����׳���ʻ10kmʱ������1��������ʻ1Сʱ��·��Ϊ80km��ȼ��Ϊ8������C����
����D����ͼ���֪���ٶ�С��80km/hʱ��������ȼ��Ч�ʴ����ҳ���ȼ��Ч�ʣ�
���ñ��������ҳ���ʡ�ͣ���D��ȷ.
��ѡ��ABC.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������![]() ��ֱ��
��ֱ��![]() ֻ��һ�������㣬��
ֻ��һ�������㣬��![]() ��������
��������![]() �ϵĶ���.
�ϵĶ���.
��1����������![]() �ķ��̣�
�ķ��̣�
��2������![]() ����֤��ֱ��
����֤��ֱ��![]() �����㣻
�����㣻
����![]() ��������
��������![]() ����ԭ�㲻�غϵĶ��㣬��
����ԭ�㲻�غϵĶ��㣬��![]() ����֤��ֱ��
����֤��ֱ��![]() ��б��Ϊ��ֵ��������ö�ֵ.
��б��Ϊ��ֵ��������ö�ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������![]() �У�
��![]() ��
��![]() ��
��![]() ƽ��ABCD��EΪPD���е㣬
ƽ��ABCD��EΪPD���е㣬![]() .
.
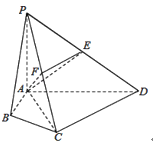
��1��������![]() �����V��
�����V��
��2����FΪPC���е㣬��֤��ƽ��![]() ƽ��AEF��
ƽ��AEF��
��3��������![]() �Ĵ�С.
�Ĵ�С.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪0��m��2,����M��������F1����m,0��,F2��m,0���ľ���֮��Ϊ4,���M�Ĺ켣Ϊ����C,������C����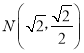 .
.
��1����m��ֵ�Լ�����C�ķ��̣�
��2��������![]() ��б�ʲ�Ϊ���ֱ��l������C����A,B����.֤������ABΪֱ����Բ������C���Ҷ���.
��б�ʲ�Ϊ���ֱ��l������C����A,B����.֤������ABΪֱ����Բ������C���Ҷ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����6����2��0��1��9��20��19����������ų�һ�У�ƴ��һ��8λ��(��λ��Ϊ0)��������IJ�ͬ��8λ���ĸ���Ϊ______ .
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ���ڵ�������![]() �У�
��![]() ��
��![]() ��
��![]() ��ֱ������
��ֱ������![]() ���ڵ�ƽ�洹ֱ��ƽ��
���ڵ�ƽ�洹ֱ��ƽ��![]() ����
����![]() ��
��![]() .
.

��1��֤����ƽ��![]() ƽ��
ƽ��![]() ��
��
��2����![]() ���߶�
���߶�![]() �ϣ���ȷ����
�ϣ���ȷ����![]() ��λ�ã�ʹƽ��
��λ�ã�ʹƽ��![]() ��ƽ��
��ƽ��![]() ���ɵĶ���ǵ�����ֵΪ
���ɵĶ���ǵ�����ֵΪ![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������![]() �ĵ���ABCD�DZ߳�Ϊa�����Σ�
�ĵ���ABCD�DZ߳�Ϊa�����Σ�![]() ��ABCD��
��ABCD��![]() ��E��F�ֱ���CD��PC���е�.
��E��F�ֱ���CD��PC���е�.

��1����֤��ƽ��![]() ƽ��PAB��
ƽ��PAB��
��2��M��PB�ϵĶ��㣬EM��ƽ��PAB���ɵ�����Ϊ![]() ��������
��������![]() ������ֵ.
������ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() �Ƕ�����R�ϵ��溯������
�Ƕ�����R�ϵ��溯������![]() ʱ��
ʱ��![]() �������������⣺
�������������⣺
�ٺ���![]() ��2����㣻
��2����㣻
��![]() �Ľ⼯Ϊ
�Ľ⼯Ϊ![]() ��
��
��![]() ��
��![]() ������
������![]() ��
��
�ܵ�![]() ʱ��
ʱ��![]() ����
����![]() .
.
����������ĸ����ǣ� ��
A.1B.2C.3D.4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() ����
���� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��ֱ��
��ֱ��![]() ��ƽ��
��ƽ��![]() ��
��![]() ����
���� ![]() Ϊ
Ϊ![]() ���е���
����� ![]() ��
�� ![]() .
.

������![]() ����֤��ƽ��
����֤��ƽ��![]() ƽ��
ƽ��![]() ��
��
������![]() ����ֱ��
����ֱ��![]() ��ƽ��
��ƽ��![]() ���ɽǵ�����ֵ��ȡֵ��Χ.
���ɽǵ�����ֵ��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com