
 ����Ϊ��������������C�ϵĵ㵽ֱ��x-y+1=0�ľ�������ֵ��
����Ϊ��������������C�ϵĵ㵽ֱ��x-y+1=0�ľ�������ֵ�� +
+ ��
�� �����ҽ���
�����ҽ��� =
= ʱ��ʽȡ�Ⱥţ����������Ͻ��ۣ�����f��x��=
ʱ��ʽȡ�Ⱥţ����������Ͻ��ۣ�����f��x��= +
+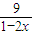 ��x��0��
��x��0�� ������Сֵ��
������Сֵ��
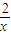 +
+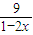 ת��Ϊf��x��=
ת��Ϊf��x��= +
+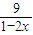 �������ø����IJ���ʽ������⣮
�������ø����IJ���ʽ������⣮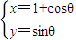 ��Ϊֱ�����귽�̵ã�x-1��2+y2=1��
��Ϊֱ�����귽�̵ã�x-1��2+y2=1��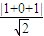 =
=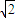 ��
�� +1��
+1��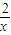 +
+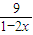 =
=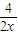 +
+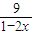 ��
��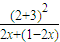 =25��
=25�� =
=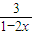 ��x=
��x=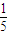 ʱȡ�Ⱥţ�
ʱȡ�Ⱥţ�

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��2012•����ģ�⣩ѡ���⣨�뿼���ڵ�16�������С������ѡ�����������ȫ������ǰ����Ƿ֣�Ҫд����Ҫ��������������̣�
��2012•����ģ�⣩ѡ���⣨�뿼���ڵ�16�������С������ѡ�����������ȫ������ǰ����Ƿ֣�Ҫд����Ҫ��������������̣�
|
| a2 |
| x |
| b2 |
| y |
| (a+b)2 |
| x+y |
| a |
| x |
| b |
| y |
| 2 |
| x |
| 9 |
| 1-2x |
| 1 |
| 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2010�꺣��ʡ������У������ѧ������ ���ͣ������
ѡ���⣺�뿼���ڵ�22��23��24������ѡһ����������������������ĵ�һ��Ƿ�
22������С������10�֣�ѡ��4��1����֤��ѡ��
��ͼ��AB�ǡ�O��ֱ����AC���ң���BAC��ƽ����AD����O�ڵ�D��DE��AC����AC���ӳ����ڵ�E��OE��AD�ڵ�F��
��I����֤��DE�ǡ�O�����ߣ�
��II���� ��ֵ.
��ֵ.

23������С������10�֣�ѡ��4��2����ϵ���������
��ֱ������ϵԭ���뼫���꼫���غϣ� x���������뼫���غϣ�����֪����C�ļ����귽��Ϊ ����F1��F2Ϊ�����ҽ��㣬ֱ��l�IJ�������Ϊ
����F1��F2Ϊ�����ҽ��㣬ֱ��l�IJ�������Ϊ
��I����ֱ��l����ͨ���̺�����C��ֱ�����귽�̣�
��II��������C�ϵĶ���P��ֱ��l�������롣
24������С������10�֣�ѡ��4��5����ʽѡ��
���������ʵ�� ���������ʵ��M�����ֵ��m��
���������ʵ��M�����ֵ��m��
��1����m��ֵ��
��2���ⲻ��ʽ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2010�꺣��ʡ������У������ѧ���ģ� ���ͣ�ѡ����
ѡ���⣺�뿼���ڵ�22��23��24������ѡһ����������������������ĵ�һ��Ƿ�
22������С������10�֣�ѡ��4��1����֤��ѡ��
��ͼ��AB�ǡ�O��ֱ����AC���ң���BAC��ƽ����AD����O�ڵ�D��DE��AC����AC���ӳ����ڵ�E��OE��AD�ڵ�F��
��I����֤��DE�ǡ�O�����ߣ�
��II���� ��ֵ.
��ֵ.

23������С������10�֣�ѡ��4��2����ϵ���������
��ֱ������ϵԭ���뼫���꼫���غϣ� x���������뼫���غϣ�����֪����C�ļ����귽��Ϊ ����F1��F2Ϊ�����ҽ��㣬ֱ��l�IJ�������Ϊ
����F1��F2Ϊ�����ҽ��㣬ֱ��l�IJ�������Ϊ
��I����ֱ��l����ͨ���̺�����C��ֱ�����귽�̣�
��II��������C�ϵĶ���P��ֱ��l�������롣
24������С������10�֣�ѡ��4��5����ʽѡ��
���������ʵ�� ���������ʵ��M�����ֵ��m��
���������ʵ��M�����ֵ��m��
��1����m��ֵ��
��2���ⲻ��ʽ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ѡ���⣨�뿼���ڵ�16�������С������ѡ�����������ȫ������ǰ����Ƿ֣�Ҫд����Ҫ��������������̣�
ѡ���⣨�뿼���ڵ�16�������С������ѡ�����������ȫ������ǰ����Ƿ֣�Ҫд����Ҫ��������������̣�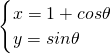 ����Ϊ��������������C�ϵĵ㵽ֱ��x-y+1=0�ľ�������ֵ��
����Ϊ��������������C�ϵĵ㵽ֱ��x-y+1=0�ľ�������ֵ��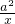 +
+ ��
�� �����ҽ���
�����ҽ��� =
=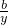 ʱ��ʽȡ�Ⱥţ����������Ͻ��ۣ�����f��x��=
ʱ��ʽȡ�Ⱥţ����������Ͻ��ۣ�����f��x��= +
+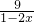 ��x��0��
��x��0�� ������Сֵ��
������Сֵ���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com